Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

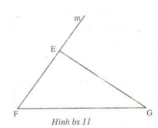
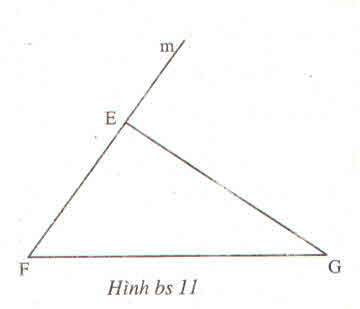
Tổng 3 góc tam giác = 180 độ => góc FEG = 180 độ - FEG - EGF
Mà FEG và GEm bù nhau => FEG = 180 độ - GEm => EFG + EGF = GEm

EFG
+
EGF
=
GEm
suy ra G+F=m dư 1
m+1=E
mình nói đến đây thôi nha vì mình học lớp 6

TL :
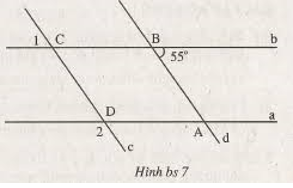
a) Vẽ thêm các tia đối của các tia Dm, Cp, Bq và An.
Vẽ thêm các đường phân giác Ds và Ar của góc ∠D và ∠A.
Khi đó chứng minh được Cp song song với Ds.
Tương tự chứng minh được Ar song song với Dm.
Từ đó suy ra được: An // Cp và Dm // Bq.
b) Sử dụng tính chất tia phân giác của hai góc bù nhau có được Ds, Dm vuông góc với nhau.
Từ đó suy ra được: An vuông góc với Bq.
Hok tốt

nh 98): Xét ΔABC và ΔABD có:
Nên ΔABC = ΔABD (g.c.g)
- Hình 99): Ta có:
Xét ΔABD và ΔACE có:
Nên ΔABD = ΔACE ( g.c.g)
Xét ΔADC và ΔAEB có:
DC = EB (Vì DC = DB + BC ; EB = EC + BC mà DB = EC)
Nên ΔADC = ΔAEB (g.c.g)
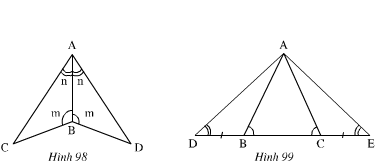
Xem hình 98)
∆ABC và ∆ABD có:
ˆA1A1^=ˆA2A2^(gt)
AB là cạnh chung.
ˆB1B1^=ˆB2B2^(gt)
Nên ∆ABC=∆ABD(g.c.g)
Xem hình 99)
Ta có:
ˆB1B1^+ˆB2B2^=1800 (Hai góc kề bù).
ˆC1C1^+ ˆC2C2^=1800 (Hai góc kề bù)
Mà ˆB2B2^=ˆC2C2^(gt)
Nên ˆB1B1^=ˆC1C1^
* ∆ABD và ∆ACE có:
ˆB1B1^=ˆC1C1^(cmt)
BD=EC(gt)
ˆDD^ = ˆEE^(gt)
Nên ∆ABD=∆ACE(g.c.g)
* ∆ADC và ∆AEB có:
ˆDD^=ˆEE^(gt)
ˆC2C2^=ˆB2B2^(gt)
DC=EB
Nên ∆ADC=∆AEB(g.c.g)

bn hương làm đ r đó bn, (tui đọc mắc cuoi wa lam k dc) chúc bn kt tot
a. Tam giác ABC có AB = AC nên là tam giác cân.
Suy ra AH là đường cao đồng thời là phân giác góc BAC.
b. Xét tam giác AHB và AHC có:
Góc AHC = Góc AHB = 90 độ
AB = AC (gt)
AH chung
=> Tam giác AHB = Tam giác AHC ( cạnh huyền - cạnh góc vuông )
C. AH vuông góc với BC theo giả thiết ?!







 cho hình vẽ trên:
cho hình vẽ trên:
Kẻ tia En song song với FG.
∠F và ∠E2 ở vị trí đồng vị ⇒ ∠F = ∠E2. (1)
∠G và ∠E1 ở vị trí so le trong ⇒ ∠G = ∠E1. (2)
Từ (1) và (2) suy ra: ∠F + ∠G = ∠E1 + ∠E2 (đpcm).
Hay ∠EFG + ∠EGF = ∠GEm.