
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

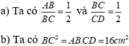

Bài 209 : đăng tách ra cho mn cùng làm nhé
a,sửa đề : \(A=\left(3x+1\right)^2-2\left(3x+1\right)\left(3x+5\right)+\left(3x+5\right)^2\)
\(=\left(3x+1-3x-5\right)^2=\left(-4\right)^2=16\)
b, \(B=\left(3+1\right)\left(3^2+1\right)\left(3^4+1\right)...\left(3^{32}+1\right)\)
\(2B=\left(3^2-1\right)\left(3^2+1\right)\left(3^4+1\right)...\left(3^{32}+1\right)=\left(3^{32}-1\right)\left(3^{32}+1\right)\)
\(2B=3^{64}-1\Rightarrow B=\frac{3^{64}-1}{2}\)
c, \(C=\left(a+b-c\right)^2+\left(a-b+c\right)^2-2\left(b-c\right)^2\)
\(=2\left(a-b+c\right)^2-2\left(b-c\right)^2=2\left[\left(a-b+c\right)^2-\left(b-c\right)^2\right]\)
\(=2\left(a-b+c-b+c\right)\left(a-b+c+b-c\right)=2a\left(a-2b+2c\right)\)

Câu hỏi của Thị Kim Vĩnh Bùi - Toán lớp 8 - Học toán với OnlineMath
Ở link trên đã tìm đc các giá trị của a, b, c, d thay vào tìm đc M = 0.

a) Xét \(\Delta AOC\) và \(\Delta BOD\) có:
\(\widehat{ACO}=\widehat{BDO}=90^o;\widehat{AOB}:chung;OA=OB\)
\(\Rightarrow\) \(\Delta AOC\) = \(\Delta BOD\) \(\Rightarrow\) \(\widehat{OAC}=\widehat{OBD}\)
b) Xét \(\Delta OAB\) có : OA = OB \(\Rightarrow\) \(\Delta OAB\) cân tại O
\(\Rightarrow\) \(\widehat{OAB}=\widehat{OBA}\)
Có \(\widehat{OAC}+\) \(\widehat{CAB}=\widehat{OAB}\) ; \(\widehat{OBD}+\widehat{DBA}=\widehat{OBA}\)
mà \(\widehat{OAB}=\widehat{OBA}\) ; \(\widehat{OAC}=\widehat{OBD}\)
\(\Rightarrow\widehat{CAB}=\widehat{DBA}\Rightarrow\Delta IAB\) cân tại I
\(\Rightarrow IA=IB\)
c) Xét \(\Delta IBC\) vuông tại C
=> IB > IC mà IB = IA
=> IA > IC
Cho góc nhọn xOy.Trên tia Ox lấy điểm A (A \(\ne\) O); trên tia Oy lấy điểm B
(B khác O) sao cho OA = OB. Kẻ AC ⊥ Oy (C ∈ Oy); BD⊥Ox (D ∈ Ox).Gọi I là giao điểm của AC và BD.
a. Chứng minh \(\Delta\) AOC = \(\Delta\) BOD
b. Chứng minh \(\Delta\) AIB cân
c. So sánh IC và IA

mỗi tỉ số đã cho đều bớt đi 1 ta được :
\(\frac{2a+b+c+d}{a}\) - 1 = \(\frac{a+2b+c+d}{b}\) - 1 = \(\frac{a+b+2c+d}{c}\) - 1 = \(\frac{a+b+c+2d}{d}\) - 1
\(\frac{a+b+c+d}{a}\) = \(\frac{a+b+c+d}{b}\) = \(\frac{a+b+c+d}{c}\) = \(\frac{a+b+c+d}{d}\)
- Nếu a+b+c+d \(\ne\) 0 thì a = b = c =d lúc đó M = 1 + 1 + 1 + 1 = 4
- Nếu a + b + c + d = 0 thì a + b = - ( c + d ) ; b + c = - ( d + a )
c + d = - ( a + b ) ; d + a = - ( b + c )
Lúc đó : M= (-1 ) + (-1) + (-1) + (-1) = -4
Lấy 1 điểm O tùy ý , Qua O vẽ 9 đường thẳng lần lượt song song với 9 đường thẳng đã cho 9 đường thẳng qua O tạo thành 18 góc không có điểm trong chung , mỗi góc này tương ứng bằng góc giữa 2 đường thẳng tronh số 9 đường thẳng đã cho . Tổng số đo của 18 góc đỉnh O là 360 độ do đó ít nhất có một góc nhỏ hơn 360 : 18 = 20 , từ đó suy ra ít nhất cũng có hai đường thẳng mà góc nhọn giữa chúng không nhỏ hơn 20 độ