Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A
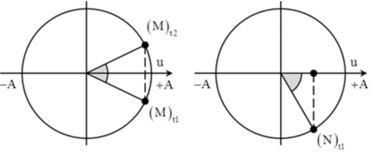
Từ hình vẽ, ta xác định được
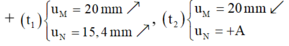
Ta có: cos α 2 = 20 A cosα = 15 , 3 A ⇒ 2 Acos 2 ( α 2 ) - 1 = 15 , 3 A
⇔ 2 ( 20 A ) 2 - 1 = 15 , 3 A ⇒ A = 21 , 6 mm .
→ Từ đây ta tìm được ω = 5 π rad / s .
→ Tốc độ cực đại v max = ωA ≈ 340 mm / s .
Chọn đáp án C
Từ hình vẽ ta xác định được: + t 1 u M = 20 m m ↑ u N = 15 , 4 m m ↑ ; t 2 u M = 20 m m ↓ u N = + A
Ta có:
cos α 2 = 20 A cos α = 15 , 3 A ⇒ 2 cos 2 α 2 − 1 = 15 , 3 A ⇔ 2 20 A 2 − 1 = 15 , 3 A ⇒ A = 21 , 6 m m
⇒ ω = 5 π r a d / s ⇒ v max = ω A = 340 m m / s
+ Từ hình vẽ ta xác định được: + t 1 u M = 20 m m ↑ u N = 15 , 4 m m ↑ ; t 2 u M = 20 m m ↓ u N = + A
+ Ta có: cos α 2 = 20 A cos α = 15 , 3 A ⇒ 2 cos 2 α 2 − 1 = 15 , 3 A ⇔ 2 20 A 2 − 1 = 15 , 3 A ⇒ A = 21 , 6 m m
⇒ ω = 5 π r a d / s ⇒ v max = ω A = 340 m m / s
Chọn đáp án C
Đáp án C
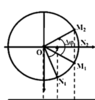
v Quy luật truyền sóng: Sườn trước đi lên, sườn sau đi xuống.
∙Tại thời điểm t1 điểm M1 (thuộc sườn trước), 
và đi theo chiều dương. Điểm N1 (thuộc sườn trước) , 
và đi theo chiều dương.
∙Tại thời điểm t2 điểm M2 (thuộc sườn sau) 
và điểm N2 lại ở biên dương. (Xem VTLG).
Chú ý: Ở trên đồ thị . M 1 = M 2 .Các bước tính toán để tìm ra w dựa vào chức năng SHIFT-SOLVE.
\(\omega=\frac{2\pi}{T}=2\pi\)(rad/s)
Vận tốc cực đại \(v_{max}=\omega A=2\pi.5=10\pi\)(cm/s)
Vì vận tốc là đại lượng biến thiên điều hòa theo thời gian, nên ta khảo sát nó bằng véc tơ quay.
10π v 5π M N -10π O
Tại thời điểm t, trạng thái của vận tốc ứng với véc tơ OM, sau 1/6 s = 1/6 T, véc tơ quay: 1/6.360 = 600
Khi đó, trạng thái của vận tốc ứng với véc tơ ON --> Vận tốc đạt giá trị cực đại là: \(10\pi\) (cm/s)
Đáp án B.
O u 3 a t M 2a
Điều kiện sóng dừng 2 đầu cố định: \(l=\frac{k\lambda}{2}\Rightarrow\lambda=l=\frac{v}{f}\Rightarrow f=\frac{v}{l}\)(Với k = 2, vì trên hình có 2 bụng).
Thời gian từ \(u=x\rightarrow u=-x\) (liên tiếp): \(5\Delta t-\Delta t=4\Delta t\)
Suy ra thời gian từ vị trí: \(u=x\rightarrow u=0\) là: \(\frac{4\Delta t}{2}=2\Delta t\)
Suy ra thời gian đi từ vị trí: \(u=2a\rightarrow u=0\) (biên về VTCB) là \(\Delta t+2\Delta t=3\Delta t=\frac{T}{4}\)
Chu kì dao động: \(T=4.3\Delta t=12\Delta t\)
Suy ra: \(A_M=x=2a.\frac{\sqrt{3}}{2}=a\sqrt{3}\) (dựa vào hình vẽ, cung \(\Delta t\) ứng với 300).
Dựa vào vòng tròn: \(V_M\) \(_{max}=a\sqrt{3}.\omega=a\sqrt{3}.2\pi f=2\pi\sqrt{3}\frac{va}{l}\)
Đáp án B
