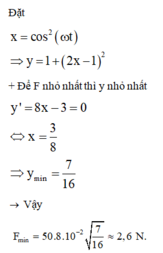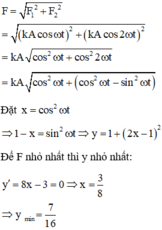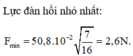Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải thích: Đáp án D
Phương pháp:
Sử dụng lí thuyết về khoảng cách của hai vật dao động điều hoà
Khảo sát hàm số bậc hai
Cách giải:
Phương trình dao động của vật A là ![]()
Phương trình dao động của vật B là ![]()
Mặt khác: 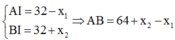
Có:
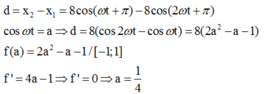
Xét bảng biến thiên sau:
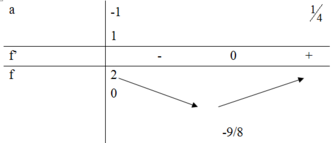
Từ bảng biến thiên ta có:
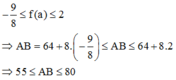

Đáp án D
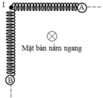
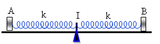
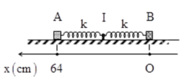
Chọn hệ trục tọa độ như hình vẽ
Phương trình dao động của mỗi vật
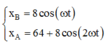
Khoảng cách giữa hai vật
![]()
Biến đổi lượng giác
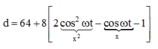
Khảo sát hàm số ta thu được
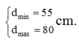

Đáp án D
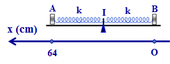
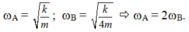
Chọn trục tọa độ Ox như hình vẽ, ta có phương trình dao động của hai vật là
xA = 64 + 8coswAt = 64 + 8cos2wBt
= 64 + 8(2cos2wBt - 1) = 56 + 16cos2wBt;
xB = 8coswBt. Khoảng cách giữa hai vật là L = y = xA – xB = 56 + 16cos2wBt - 8coswBt
Đặt coswBt = x với – 1 £ x = coswBt £ 1, ta có y = 56 + 16x2 – 8x
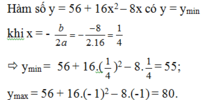

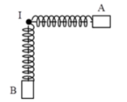
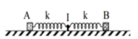
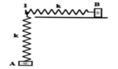
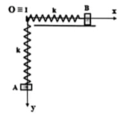
Các điểm trên lò xo thỏa mãn: \(OM = MN = NI = 10cm.\)
Tỉ số lực kéo lớn nhất và lực kéo nhỏ nhất tác dụng lên điểm treo O của lò xo chính là
\(\frac{F_{đhmax}}{F_{đhmin}} = \frac{k(\Delta l +A)}{k(\Delta l -A)}=3 => \Delta l = 2A.(1)\)
Lò xo dãn đều, khoảng cách lớn nhất giữa hai điểm M, N là 12 cm
=> Độ dãn lớn nhất của cả lò xo là \(\Delta l + A = 3.(12-10) = 6cm. (2)\)
Từ (1) và (2) ta có: \(\Delta l = 4cm = 0,04m.\)
\(T = 2\pi \sqrt{\frac{\Delta l }{g}} = 2\sqrt{\Delta l} = 0,4s.\)
\(f = \frac{1}{T} = 2,5Hz. \)
cho em hỏi : chỗ mà độ dãn lớn nhất của lò xo sao lại ra được vầy ạ ??

Chọn C.
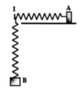
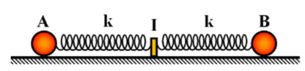
Gắn trục Oxy vào hệ, gốc tạo độ O ≡ I

= 40 + 10 cos ω t + π 2 + 30 + 5 cos ω t 2


Khi vật I qua VTCB thì nó có vận tốc là: \(v=\omega.A\)
Khi thả nhẹ vật II lên trên vật I thì động lượng được bảo toàn
\(\Rightarrow M.v = (M+m)v'\Rightarrow v'=\dfrac{3}{4}v\)
Mà \(v'=\omega'.A'\)
\(\dfrac{v'}{v}=\dfrac{\omega'}{\omega}.\dfrac{A'}{A}=\sqrt{\dfrac{M}{\dfrac{4}{3}M}}.\dfrac{A'}{A}=\dfrac{3}{4}\)
\(\Rightarrow \dfrac{A'}{A}=\dfrac{\sqrt 3}{2}\)
\(\Rightarrow A'=5\sqrt 3cm\)
Chọn A.
Vận tốc của M khi qua VTCB: v = ωA = 10.5 = 50cm/s
Vận tốc của hai vật sau khi m dính vào M: v’ = Mv/(M+v)= 40cm/s
Cơ năng của hệ khi m dính vào M: W = 1/2KA'2= 1/2(m+M)v'2
A’ = 2căn5