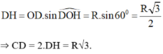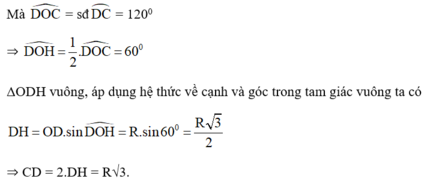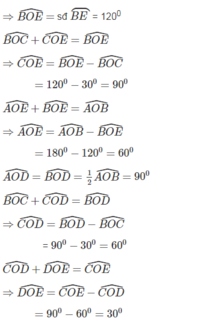Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

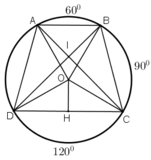
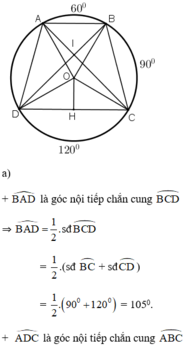
ˆBAD=900+12002=1050BAD^=900+12002=1050 (góc nội tiếp chắn cung BCD) (1)
ˆADC=600+9002=750ADC^=600+9002=750 ( góc nội tiếp chắn cung ABC) (2)
Từ (1) và (2) có:
ˆBAD+ˆADC=1050+750=1800BAD^+ADC^=1050+750=1800 (3)
ˆBADBAD^ và ˆADCADC^ là hai góc trong cùng phía tạo bởi cát tuyến AD và hai đường thẳng AB, CD.
Đẳng thức (3) chứng tỏ AB // CD. Do đó tứ giác ABCD là hình thang, mà hình thang nội tiếp là hình thang cân.
Vậy ABCD là hình thang cân (BC = AD và sđ cung BC = AD = 90o )
b) Giả sử hai đường chéo AC và BD cắt nhau tại I.
ˆCIDCID^ là góc có đỉnh nằm trong đường tròn, nên:
ˆCID=sđcungAB+sđcungCD2=600+12002=900CID^=sđcungAB+sđcungCD2=600+12002=900
Vậy AC ⊥ BD
c)
Vì sđ cung AB = 60o nên ˆAIB=600AIB^=600 => ∆AIB đều, nên AB = R
Vì sđ cung BC = 90o nên BC = R√2
AD = BC = R√2
nên sđ cung CD= 120o nên CD = R√3
Hướng dẫn giải:
ˆBAD=900+12002=1050BAD^=900+12002=1050 (góc nội tiếp chắn cung BCD) (1)
ˆADC=600+9002=750ADC^=600+9002=750 ( góc nội tiếp chắn cung ABC) (2)
Từ (1) và (2) có:
ˆBAD+ˆADC=1050+750=1800BAD^+ADC^=1050+750=1800 (3)
ˆBADBAD^ và ˆADCADC^ là hai góc trong cùng phía tạo bởi cát tuyến AD và hai đường thẳng AB, CD.
Đẳng thức (3) chứng tỏ AB // CD. Do đó tứ giác ABCD là hình thang, mà hình thang nội tiếp là hình thang cân.
Vậy ABCD là hình thang cân (BC = AD và sđ cung BC = AD = 90o )
b) Giả sử hai đường chéo AC và BD cắt nhau tại I.
ˆCIDCID^ là góc có đỉnh nằm trong đường tròn, nên:
ˆCID=sđcungAB+sđcungCD2=600+12002=900CID^=sđcungAB+sđcungCD2=600+12002=900
Vậy AC ⊥ BD
c)
Vì sđ cung AB = 60o nên ˆAIB=600AIB^=600 => ∆AIB đều, nên AB = R
Vì sđ cung BC = 90o nên BC = R√2
AD = BC = R√2
nên sđ cung CD= 120o nên CD = R√3

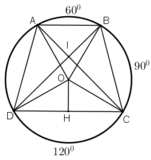


=> AB//CD (hai góc trong cùng phía bù sau)
=> ABCD là hình thang.


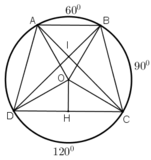
+ ∆ O A B có

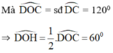
∆ O D H vuông, áp dụng hệ thức về cạn và góc trong tam giác vuông ta có