Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Từ dữ kiện đề bài ta suy ra cuộn dây có điện trở thuần, với loại bài toán liên quan đến độ lệch pha ta nên vẽ giản đồ véc-tơ:

Ta có: $\widehat{\vec{MB}; \vec{AM}}=60^0$
Mặt khác $\begin{cases} \widehat{\vec{AB};\vec{AM}}=30^0 =\dfrac{1}{2}\widehat{\vec{MB}; \vec{AM}} \\ \widehat{\vec{MB}; \vec{AM}}= \widehat{MAB}+ \widehat{ABM} \end{cases}$
Suy ra $\Delta MAB$ cân tại $M$
Khi đó:
$U_r+U_r=U_{U_{AB}}. \cos 30^0$
Do: $U_r=U_R \cos 60^0$ nên:
$U_R=U_{AM}=\dfrac{U_{AB}\cos 30^0}{1+ \cos 60^0}=80 \sqrt{3} V$

\(2LC\omega^2=1\rightarrow2Z_L=Z_C\rightarrow2u_L=-uc\)
\(u_m=u_R+u_L+u_c=40+\left(-30\right)+60=70V\)
Chọn B

\(U_{RC}=const=U\) khi \(Z_{L1}=2Z_C=R\)
Mặt khác L thay đổi để : \(U_{Lmax}:U_{Lmax}=\frac{U\sqrt{R^2+Z^2_C}}{R}=\frac{U\sqrt{2^2+1}}{2}=\frac{U\sqrt{5}}{2}\)
\(\Rightarrow chọn.D\)
+,có C=C1=>U_R=\frac{U.R}{\sqrt{R^2+(Zl-ZC1)^2}}
+,U R ko đổi =>Zl=ZC1
+,có c=C1/2=>ZC=2ZC1
=>U(AN)=U(RL)=\frac{U\sqrt{r^2+Z^2l}}{\sqrt{R^2+(Zl-2Z^2C1)}}=u=200V

Chọn C
Δ MNB : MN = U R = MB · sin 30 ° = 40 3 Δ AEN ⇒ EN = AN · cos 30 ° = 60 3 ( V ) ⇒ U r = EN - MN = 20 3 ⇒ r R = U r U R = 1 2 ⇒ r = R 2 = 30 W

Đáp án C.
lúc đầu ta có :
UMB=2UR => ZMB=2R <=> ZC=\(\sqrt{3}\)R mà C=\(\frac{L}{R^2}\) => ZL=\(\frac{R}{\sqrt{3}}\)
lúc sau ta có Uc' max :
Zc'.ZL=R2+ \(Z^2_L\) => Zc'=\(\frac{4R}{\sqrt{3}}\)
\(\text{tanφ}=\frac{Z_L-Z_C}{R}\Rightarrow\tan\varphi=-\sqrt{3}\Rightarrow\varphi=-\frac{\pi}{3}\)
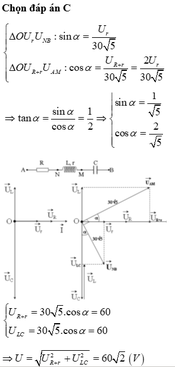


Đáp án C
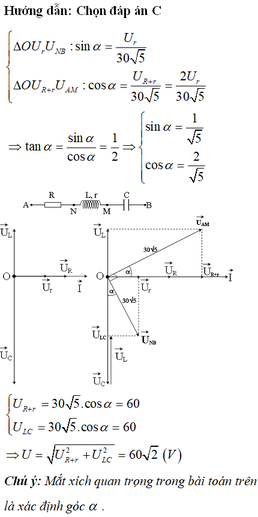
Ta có r = R →Ur = UR→UR+r = 2Ur
∆ O U r U N B : sin α = U r 30 5 ∆ O U R + r U A M : cos α = U R + r 30 5 = 2 U r 30 5 ⇒ tan α = sin α cos α = 1 2 ⇒ sin α = 1 5 cos α = 2 5 U R + r = 30 5 . cos α = 60 U L C = 30 5 . cos α = 60 ⇒ U = U R + r 2 + U L C 2 = 60 2 ( V )