

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Theo công thức liên hệ chiều dài day và số bụng sóng ta có $2,4=8.\dfrac{\lambda}{2} \Rightarrow \lambda =0,6m=60 cm$
Công thức tính biên độ tại một điểm bất kì trên sợi dây cách nút gần nhất một khoảng là d đang có sóng dừng với biên độ tại bụng là 2A:
$a=2A \cos \left(\dfrac{2 \pi d}{\lambda} +\dfrac{\pi }{2} \right).$
Gọi khoảng cách từ A tới nút gần nhất là d thì do $\dfrac{\lambda}{4}<20$ nên ta có B cách nút gần nhất với nó một khoảng 10-d.
$| a_A-a_B |=2A |\left(\dfrac{2 \pi d}{\lambda} +\dfrac{\pi }{2} \right)-\left(\dfrac{2 \pi \left(10-d\right)}{\lambda} +\dfrac{\pi }{2} \right) |$
$=4A |\sin \left(\dfrac{10 \pi }{\lambda}+\dfrac{\pi }{2} \right) | |\sin \left(\dfrac{\pi \left(2x-10\right)}{\lambda}\right) |.$
Biểu thức trên lớn nhất khi $|\sin \left(\dfrac{\pi \left(2x-10\right)}{\lambda}\right) |$ lớn nhất, tức là bằng 1.
Thay số ta có đáp án D


Đáp án A
+ Khi có sóng dừng, phần tử dây cách nút một đoạn d dao dộng với biên độ a = A sin 2 π d λ , phần tử dây cách bụng một đoạn d dao động với biên độ a = A cos 2 π d λ .
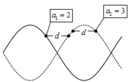
+ Với a 2 = 3 mm, lớn hơn a 1 = 2 mm → hai điểm gần nhau nhất dao động cùng biên độ a 2 phải đối xứng nhau qua bụng sóng, hai điểm dao động với cùng biên độ a 1 phải đối xứng nhau qua nút sóng
→ a 1 = A sin π d 2 a 2 = A cos π d 2 ↔ 2 = A sin 10 π λ 3 = A c o s 10 π λ → A = 2 2 + 3 2 = 13 λ = 53 mm.
+ Khoảng cách giữa hai nút sóng liên tiếp là Δ d = λ 2 = 26 , 7 m m

Chọn đáp án B
Trên hình 3λ/4 = 30 cm → λ = 40 cm.
Từ t 1 đến t 2 hết 2/3: Điểm M đi từ biên dương sang biên âm rồi quay lại vị trí –A/2.
Vẽ trên đường tròn lượng giác từ t 1 đến t 2 hết 2/3 s: đi được góc = 240 ° → 2T/3 = 2/3 → T = 1 s.
→ v = λ/T = 40/1 = 40 cm/s.

Đáp án B
Trên hình 3λ/4 = 30 cm → λ = 40 cm.
Từ t1 đến t2 hết 2/3: Điểm M đi từ biên dương sang biên âm rồi quay lại vị trí –A/2.
Vẽ trên đường tròn lượng giác từ t1 đến t2 hết 2/3 s: đi được góc = 2400 → 2T/3 = 2/3 → T = 1 s.
→ v = λ/T = 40/1 = 40 cm/s.

+ Ta biễu diễn vị trí của M và N trên đường tròn.

Từ hình vẽ, ta thấy rằng có hai khả năng xảy ra của độ lệch pha


Đáp án B
Ta có: l = k λ 2 = k v 2 f ⇒ f = k v 2 l = k . 40 2 . 1 , 5 = 40 3 k
Tần số có giá trị từ 30Hz đến 100Hz ⇒ 30 ≤ 40 3 k ≤ 100 ⇒ 2 , 25 ≤ k ≤ 7 , 5 ⇒ k = 3 ; 4 ; 5 ; 6 ; 7
Để tạo được sóng dừng trên dây với số nút nhiều nhất (ứng với k = 7) thì ⇒ f = 40 3 . 7 = 93 , 33 H z

Góc MOA và NOA biểu diễn ''độ lệch pha biên độ'' của M; N với điểm bụng bụng gần nó nhât. Gọi d là khoảng cách từ 1 điểm đến điểm bụng gần nó nhất khi đó độ lệch pha biên độ được tính.
\(\Delta\)φ=\(\frac{2\pi\text{d}}{\text{λ}}\text{ }\)
Theo bài ra:
\(\begin{cases}\frac{1}{20}\left(s\right)=\frac{T}{4}\\\frac{1}{15}\left(s\right)=\frac{T}{3}\end{cases}\leftrightarrow\begin{cases}\text{∠}-MOM=\frac{2\pi}{4}=\frac{\pi}{2}\\\text{∠}-NON=\frac{2\pi}{3}\end{cases}\)
\(\rightarrow\begin{cases}MOA=\frac{\pi}{4}\\NOA=\frac{\pi}{6}\end{cases}\) \(\leftrightarrow\begin{cases}2\pi\frac{MP}{\text{λ}}=\frac{\pi}{4}\\2\pi\frac{NP}{\text{λ}}=\frac{\pi}{6}\end{cases}\) \(\leftrightarrow\begin{cases}MP=\frac{\text{λ}}{8}\\NP=\frac{\text{λ}}{12}\end{cases}\)
\(\Rightarrow\frac{\text{λ}}{8}-\frac{\text{λ}}{12}=0,2\leftrightarrow\text{λ}=4,8cm\)
2πdλ