




Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.






a/
Đặt \(cosx=t\Rightarrow0< t\le1\)
\(\Rightarrow t^2-2mt+4\left(m-1\right)=0\)
\(\Leftrightarrow t^2-4-2m\left(t-2\right)=0\)
\(\Leftrightarrow\left(t-2\right)\left(t+2-2m\right)=0\)
\(\Leftrightarrow t=2m-2\)
\(\Rightarrow0< 2m-2\le1\Rightarrow1< m\le\frac{3}{2}\)
b.
\(x\in\left(-\frac{\pi}{2};\frac{\pi}{2}\right)\Rightarrow\frac{x}{2}\in\left(-\frac{\pi}{4};\frac{\pi}{4}\right)\)
Đặt \(sin\frac{x}{2}=t\Rightarrow-\frac{\sqrt{2}}{2}< t< \frac{\sqrt{2}}{2}\)
\(\Rightarrow4t^2+2t+m-2=0\Leftrightarrow4t^2+2t-2=-m\)
Xét \(f\left(t\right)=4t^2+2t-2\) trên \(\left(-\frac{\sqrt{2}}{2};\frac{\sqrt{2}}{2}\right)\)
\(f\left(-\frac{\sqrt{2}}{2}\right)=-\sqrt{2}\) ; \(f\left(\frac{\sqrt{2}}{2}\right)=\sqrt{2}\) ; \(f\left(-\frac{1}{4}\right)=-\frac{9}{4}\)
\(\Rightarrow-\frac{9}{4}\le f\left(t\right)< \sqrt{2}\Rightarrow-\frac{9}{4}\le-m< \sqrt{2}\)
\(\Rightarrow-\sqrt{2}< m\le\frac{9}{4}\)

1.
Hàm tuần hoàn với chu kì \(2\pi\) nên ta chỉ cần xét trên đoạn \(\left[0;2\pi\right]\)
\(y'=\frac{-4}{\left(cosx-2\right)^2}.sinx=0\Leftrightarrow x=k\pi\)
\(\Rightarrow x=\left\{0;\pi;2\pi\right\}\)
\(y\left(0\right)=-3\) ; \(y\left(\pi\right)=\frac{1}{3}\) ; \(y\left(2\pi\right)=-3\)
\(\Rightarrow\left\{{}\begin{matrix}M=\frac{1}{3}\\m=-3\end{matrix}\right.\)
\(\Rightarrow9M+m=0\)
2.
\(\Leftrightarrow y.cosx+y.sinx+2y=2k.cosx+k+1\)
\(\Leftrightarrow y.sinx+\left(y-2k\right)cosx=k+1-2y\)
Theo điều kiện có nghiệm của pt lượng giác bậc nhất:
\(\Rightarrow y^2+\left(y-2k\right)^2\ge\left(k+1-2y\right)^2\)
\(\Leftrightarrow2y^2-4k.y+4k^2\ge4y^2-4\left(k+1\right)y+\left(k+1\right)^2\)
\(\Leftrightarrow2y^2-4y-3k^2+2k+1\le0\)
\(\Leftrightarrow2\left(y-1\right)^2\le3k^2-2k+1\)
\(\Leftrightarrow y\le\sqrt{\frac{3k^2-2k+1}{2}}+1\)
\(y_{max}=f\left(k\right)=\frac{1}{\sqrt{2}}\sqrt{3k^2-2k+1}+1\)
\(f\left(k\right)=\frac{1}{\sqrt{2}}\sqrt{3\left(k-\frac{1}{3}\right)^2+\frac{2}{3}}+1\ge\frac{1}{\sqrt{3}}+1\)
Dấu "=" xảy ra khi và chỉ khi \(k=\frac{1}{3}\)
Đáp án A

Câu 1 với câu 2 sai đề, sin và cos nằm trong [-1;1], mà căn 2 với căn 3 lớn hơn 1 rồi
3/ \(\sin x=\cos2x=\sin\left(\frac{\pi}{2}-2x\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{2}-2x+k2\pi\\x=\pi-\frac{\pi}{2}+2x+k2\pi\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{6}+k\frac{2}{3}\pi\\x=-\frac{\pi}{2}+k2\pi\end{matrix}\right.\)
4/ \(\Leftrightarrow\cos^2x-2\sin x\cos x=0\)
Xét \(\cos x=0\) là nghiệm của pt \(\Rightarrow x=\frac{\pi}{2}+k\pi\)
\(\cos x\ne0\Rightarrow1-2\tan x=0\Leftrightarrow\tan x=\frac{1}{2}\Rightarrow x=...\)
5/ \(\Leftrightarrow\sin\left(2x+1\right)=-\cos\left(3x-1\right)=\cos\left(\pi-3x+1\right)=\sin\left(\frac{\pi}{2}-\pi+3x-1\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+1=\frac{\pi}{2}-\pi+3x-1\\2x+1=\pi-\frac{\pi}{2}+\pi-3x+1\end{matrix}\right.\Leftrightarrow....\)
6/ \(\Leftrightarrow\cos\left(\pi\left(x-\frac{1}{3}\right)\right)=\frac{1}{2}\Leftrightarrow\pi\left(x-\frac{1}{3}\right)=\pm\frac{\pi}{3}+k2\pi\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\frac{1}{3}=\frac{1}{3}+2k\Rightarrow x=\frac{2}{3}+2k\left(1\right)\\x-\frac{1}{3}=-\frac{1}{3}+2k\Rightarrow x=2k\left(2\right)\end{matrix}\right.\)
\(\left(1\right):-\pi< x< \pi\Rightarrow-\pi< \frac{2}{3}+2k< \pi\) (Ủa đề bài sai hay sao ý nhỉ?)
7/ \(\Leftrightarrow\left[{}\begin{matrix}5x+\frac{\pi}{3}=\frac{\pi}{2}-2x+\frac{\pi}{3}\\5x+\frac{\pi}{3}=\pi-\frac{\pi}{2}+2x-\frac{\pi}{3}\end{matrix}\right.\Leftrightarrow...\)
Thui, để đây bao giờ...hết lười thì làm tiếp :(
7)
\(sin\left(5x+\frac{\pi}{3}\right)=cos\left(2x-\frac{\pi}{3}\right)\)
\(\Leftrightarrow sin\left(5x+\frac{\pi}{3}\right)=sin\left(\frac{\pi}{2}-2x-\frac{\pi}{3}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}5x+\frac{\pi}{3}=\frac{\pi}{2}-2x-\frac{\pi}{3}+k2\pi\\5x+\frac{\pi}{3}=\pi-\left(\frac{\pi}{2}-2x-\frac{\pi}{3}\right)+k2\pi\end{matrix}\right.\left(k\in Z\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{-\pi}{42}+k\frac{2\pi}{7}\\x=\frac{\pi}{6}+k\frac{2\pi}{3}\end{matrix}\right.\left(k\in Z\right)\)
Do:\(0< x< \pi\)
\(Với:x=\frac{-\pi}{42}+k\frac{2\pi}{7}\left(k\in Z\right)\Rightarrow khôngtìmđượck\)
\(Với:x=\frac{\pi}{6}+k\frac{2\pi}{3}\left(k\in Z\right)\Leftrightarrow\frac{1}{4}< k< \frac{5}{4}\Rightarrow k=\left\{0;1\right\}\Rightarrow\left[{}\begin{matrix}k=0\Rightarrow x=\frac{\pi}{6}\\k=1\Rightarrow x=\frac{5\pi}{6}\end{matrix}\right.\)
Vậy nghiệm của pt là: \(x=\frac{\pi}{6};x=\frac{5\pi}{6}\)

a) cosx - √3sinx = √2 ⇔ cosx - tan![]() sinx = √2
sinx = √2
⇔ cos![]() cosx - sin
cosx - sin![]() sinx = √2cos
sinx = √2cos![]() ⇔ cos(x +
⇔ cos(x + ![]() ) =
) = ![]()
⇔ 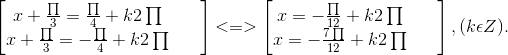
b) 3sin3x - 4cos3x = 5 ⇔ ![]() sin3x -
sin3x - ![]() cos3x = 1.
cos3x = 1.
Đặt α = arccos![]() thì phương trình trở thành
thì phương trình trở thành
cosαsin3x - sinαcos3x = 1 ⇔ sin(3x - α) = 1 ⇔ 3x - α = ![]() + k2π
+ k2π
⇔ x = ![]() , k ∈ Z (trong đó α = arccos
, k ∈ Z (trong đó α = arccos![]() ).
).

uốn giải bài này nhanh bạn cần biết đến công thức
PT:a.sinx +b.cosx =c có nghiệm khi:a2+b2≥c2a2+b2≥c2
ADCT:(m−1)2+m2≥3−2m(m−1)2+m2≥3−2m
⇔m2≥1⇔m2≥1
[m≥1m≤−1