
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

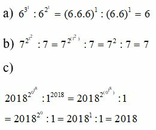

a) 1 - 2 + 3 - 4 + 5 - 6 + .....+ 25 - 26
= (1 - 2) + (3 - 4) + (5 - 6) + .....+ (25 - 26)
= -1 + (-1) + ( -1 ) +...+ ( -1 ) {có 13 số )
= -13
b) tương tự nhé bn

\(A=1+7+7^2+7^3+...+7^{2016}\)
\(\Rightarrow7A=7\left(1+7+7^2+7^3+...+7^{2016}\right)\)
\(7A=7+7^2+7^3+7^4+...+7^{2017}\)
\(\Rightarrow7A-A=\left(7+7^2+7^3+...+7^{2017}\right)-\left(1+7+7^2+...+7^{2016}\right)\)
\(\Rightarrow6A=7^{2017}-1\)
\(\Rightarrow A=\dfrac{7^{2017}-1}{6}\)

a)
⇒ \(\frac{11x-1}{4}=\frac{10}{4}\)
⇒ 11x - 1 = 10
11x = 10 + 1 = 11
x = 11 : 11 = 1
b)
\(\left[{}\begin{matrix}3x-6=0\\\frac{x}{9}-\frac{1}{3}=0\end{matrix}\right.\) ⇒ \(\left[{}\begin{matrix}3x=0+6\\\frac{x}{9}=0+\frac{1}{3}\end{matrix}\right.\)⇒ \(\left[{}\begin{matrix}3x=6\\\frac{x}{9}=\frac{1}{3}\end{matrix}\right.\)⇒ \(\left[{}\begin{matrix}x=6:3\\\frac{x}{9}=\frac{3}{9}\end{matrix}\right.\)⇒\(\left[{}\begin{matrix}x=2\\x=3\end{matrix}\right.\)
Vậy x = 2 hoặc x = 3
c)
\(M=c\left(\frac{5}{7}+\frac{7}{14}-\frac{17}{14}\right)\)
\(M=c\left(\frac{10}{14}+\frac{7}{14}-\frac{17}{14}\right)\)
\(M=\left(\frac{2018}{2019}-\frac{2019}{2020}\right).0\)
M = 0
d)
\(N=\frac{-7}{13}+2-\frac{19}{13}+\frac{2020}{2018}.\frac{2018}{202}\)
\(N=\left(\frac{-7}{13}-\frac{19}{13}\right)+2+10\)
N = \(-2+2+10\)
N = 10

219 - 7 . ( x+1) = 100
7 . ( x + 1 ) = 219 - 100 = 119
x+ 1= 119:7= 17
x = 17-1=16
(3x - 6 ). 3100 = 3103 2018x-3 = 2018
3x - 6 = 3103 : 3100 2018x-3 = 20181
3x - 6 = 33 =27 Do x-3=1 cho nên suy ra x=4
3x = 27 + 6
3x = 33
x = 33:3
x = 11

1) Đặt dãy trên là \(A\)
Theo bài ra ta có :
\(A=\frac{1}{3.3}+\frac{1}{4.4}+\frac{1}{5.5}+\frac{1}{6.6}+...+\frac{1}{100.100}\)
\(\Rightarrow A< \frac{1}{2.3}+\frac{1}{3.4}+\frac{1}{4.5}+\frac{1}{5.6}+...+\frac{1}{99.100}\)
\(\Rightarrow A< \frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+\frac{1}{5}-\frac{1}{6}+...+\frac{1}{99}-\frac{1}{100}\)
\(\Rightarrow A< \frac{1}{2}-\frac{1}{100}< \frac{1}{2}\left(đpcm\right)\)
2) \(A=\frac{5^{2018}-2017+1}{5^{2018}-2017}=\frac{5^{2018}-2017}{5^{2018}-2017}+\frac{1}{5^{2018}-2017}=1+\frac{1}{5^{2018}-2017}\)( 1 )
\(B=\frac{5^{2018}-2019+1}{5^{2018}-2019}=\frac{5^{2018}-2019}{5^{2018}-2019}+\frac{1}{5^{2018}-2019}=1+\frac{1}{5^{2018}-2019}\)( 2 )
Từ ( 1 ) và ( 2 ) \(\Rightarrow\)\(A=1+\frac{1}{5^{2018}-2017}< 1+\frac{1}{5^{2018}-2019}=B\)
\(\Rightarrow A< B\)
Vậy \(A< B.\)
1) Ta có B =
\(\frac{1}{3^2}+\frac{1}{4^2}+...+\frac{1}{100^2}\) < \(\frac{1}{1.3}+\frac{1}{3.4}+...+\frac{1}{99.100}=1-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{99}-\frac{1}{100}\)= \(\frac{99}{100}\)
=> B < 1 ( chứ không phải \(\frac{1}{2}\) bạn nhé)
Sai thì thôi chứ mk chỉ làm rờ thôi

\(A=\frac{\left(2018+1\right).2018}{2}=2037171\)
\(B=1.2+2.3+3.4+...+2018.2019\)
\(3B=1.2.3+2.3.3+3.4.3+...+2018.2019.3\)
\(3B=1.2.3+2.3.\left(4-1\right)+3.4.\left(5-2\right)+...+2018.2019.\left(2020-2017\right)\)
\(3B=1.2.3+2.3.4-1.2.3+...+2018.2019.2020-2017.2018.2019\)
\(3B=2018.2019.2020\)
\(B=\frac{2018.2019.2020}{3}\)
\(B=2743390280\)
Chúc bạn học tốt ~