


Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Phương pháp:
Công thức tính thể tích khối chóp có diện tích đáy S và chiều cao h là: V = 1 3 S h
Cách giải:

Đáp án D
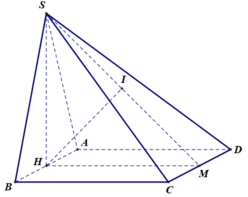
Gọi H,M lần lượt là trung điểm của AB và CD
Vì Δ S A B đều và mặt phẳng S A B ⊥ A B C D ⇒ S H ⊥ A B C D .
Ta có
C D ⊥ H M C D ⊥ S H ⇒ C D ⊥ S H M (1)
Gọi I là hình chiếu vuông góc của H lên mặt phẳng S C D (2)
Từ (1) và (2) suy ra H I ⊥ S C D
Vì A B // C D ⇒ A B // S C D ⇒ d A , S C D = d H , S C D = H I = 3 a 7 7
Giải sử A B = x x > 0 ⇒ S H = x 3 2 H M = x .
Mặt khác: 1 H I 2 = 1 H M 2 + 1 S H 2 ⇔ 7 9 a 2 = 1 x 2 + 4 3 x 2 ⇔ x 2 = 3 a 2 ⇒ x = 3 a
Thể tích: V S . A B C D = 1 3 S H . S A B C D = 1 3 . 3 a 2 .3 a 2 = 3 a 3 2 (đvtt)

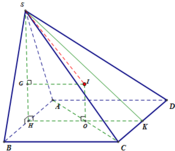
Gọi H là trung điểm của AB, suy ra A H ⊥ A B C D .
Gọi G là trọng tâm tam giác ∆SAB và O là tâm hình vuông ABCD.
Từ G kẻ GI//HO suy ra GI là trục đường tròn ngoại tiếp tam giác ∆SAB và từ O kẻ OI//SH thì OI là trục đường tròn ngoại tiếp hình vuông ABCD.
Ta có hai đường này cùng nằm trong mặt phẳng và cắt nhau tại I.
Suy ra I là tâm mặt cầu ngoại tiếp hình chóp S.ABCD.
R = S I = S G 2 + G I 2 = a 21 6 .
Suy ra thể tích khối cầu ngoại tiếp khối chóp S.ABCD là V = 4 3 π R 3 = 7 21 54 π a 3
Đáp án A

Đáp án D
Gọi M là trung điểm của AB
=> S M ⊥ A B ⇒ S M ⊥ A B C D S M = a 3 2 ⇒ V = 1 3 . S M . A B . A D = 1 3 . a 3 2 . a . a = a 3 3 6

Đáp án là A
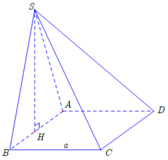
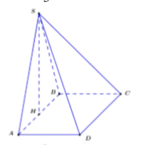
Gọi H là trung điểm A B .
Ta có S A B ⊥ A B C D S A B ∩ A B C D = A B S H ⊂ S A B ; S H ⊥ A B ⇒ S H ⊥ A B C D .
Khi đó: V S . A B C D = 1 3 S H . S A B C D = 1 3 . a 3 2 . a 2 = a 3 3 6 .