

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

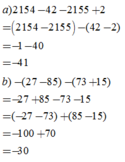


S = 101 + (-102) + 103 + (-104) + ... + 2017 + (-2018)
Khi số âm là số nguyên, ta có số số hạng là:
(2018 - 101) : 1 + 1 = 1918 (số hạng)
S = [101 + (-102)] + [103 + (-104)] + ... + [2017 + (-2018)]
S = (- 1) + (-1) + ... + (-1)
Có số số hạng là:
1918 : 2 = 959 (số hạng)
S = (-1) \(\times\) 959
S = - 959
P=(1-2-3+4)+(5-6-7+8)+...+(97-98-99+100)
=0+0+...+0
=0

a) 11-12+13-14+15-16+17-18+19-20
= -1 + ( -1 )+ ( -1 )+ ( -1 )+ ( -1 )
= -1 . 5
= -5
b) 101-102-(-103)-104-(105)-106-(107)-108-(-109)-110
= -1 + ( -1 )+ ( -1 )+ ( -1 )+ ( -1 )
= -1 . 5
= -5

A = \(\frac{1}{101^2}+\frac{1}{102^2}+\frac{1}{103^2}+\frac{1}{104^2}+\frac{1}{105^2}\)< \(\frac{1}{100.101}+\frac{1}{101.102}+\frac{1}{102.103}+\frac{1}{103.104}+\frac{1}{104.105}\) =\(\frac{1}{100}-\frac{1}{101}+\frac{1}{101}-\frac{1}{102}+\frac{1}{102}-\frac{1}{103}+\frac{1}{103}-\frac{1}{104}+\frac{1}{104}-\frac{1}{105}\)
= \(\frac{1}{100}-\frac{1}{105}=\frac{1}{2100}\)= \(\frac{1}{2^2.3.5^2.7}\)= B
Vậy A < B
\(A<\frac{1}{100.101}+\frac{1}{101.102}+\frac{1}{102.103}+\frac{1}{103.104}+\frac{1}{104.105}=\frac{1}{100}-\frac{1}{105}=\frac{1}{2100}\)
B = 1/2100
=> A< B

a )\(\frac{13}{15}+\frac{4}{7}-\frac{101}{105}\)
\(=\frac{91}{105}+\frac{60}{105}-\frac{101}{105}\)
\(=\frac{50}{105}\)
\(=\frac{10}{21}\)
b ) \(\frac{2}{5}+\frac{3}{5}\cdot\frac{4}{5}\)
\(=\frac{2}{5}+\frac{12}{25}\)
\(=\frac{10}{25}+\frac{12}{25}\)
\(=\frac{22}{25}\)
c )\(\frac{254\cdot399-145}{254+399\cdot253}\)
\(=\frac{253\cdot399+399-145}{254+399\cdot253}\)
\(=\frac{253\cdot399+254}{254+399\cdot253}\)
\(=1\)
d )\(\frac{5932+6001\cdot5931}{5932\cdot6001-69}\)
\(=\frac{5932+6001\cdot5931}{5931\cdot6001+6001-69}\)
\(=\frac{5932+6001\cdot5931}{5931\cdot6001+5932}\)
\(=1\)
e )\(\frac{1}{5}\div\frac{2}{7}\)
\(=\frac{1}{5}\cdot\frac{7}{2}\)
\(=\frac{7}{10}\)
hok tốt nha