
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

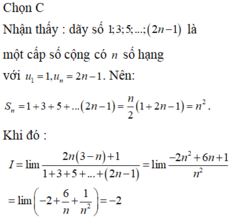

\(a=\lim\limits_{x\rightarrow2}\frac{\sqrt[3]{8x+11}-3+3-\sqrt{x+7}}{\left(x-1\right)\left(x-2\right)}=\lim\limits_{x\rightarrow2}\frac{\frac{8\left(x-2\right)}{\sqrt[3]{\left(8x+11\right)^2}+3\sqrt[3]{8x+11}+9}-\frac{x-2}{9+\sqrt{x+7}}}{\left(x-1\right)\left(x-2\right)}\)
\(=\lim\limits_{x\rightarrow2}\frac{\frac{8}{\sqrt[3]{\left(8x+11\right)^2}+3\sqrt[3]{8x+11}+9}-\frac{1}{9+\sqrt{x+7}}}{x-1}=\frac{29}{36}\)
\(b=\lim\limits_{x\rightarrow+\infty}\frac{x^2\left(2-\frac{3}{x}\right)^2.x^3\left(4+\frac{7}{x}\right)^3}{x^3\left(3+\frac{1}{x^3}\right).x^2\left(10+\frac{9}{x^2}\right)}=\frac{2.4}{3.10}=\frac{4}{15}\)
\(c=\lim\limits_{x\rightarrow0}\frac{\sqrt{1+4x}-\left(2x+1\right)+\left(2x+1-\sqrt[3]{1+6x}\right)}{x^2}\)
\(=\lim\limits_{x\rightarrow0}\frac{\frac{-4x^2}{\sqrt{1+4x}+2x+1}+\frac{8x^3+12x^2}{\left(2x+1\right)^2+\left(2x+1\right)\sqrt[3]{1+6x}+\sqrt[3]{\left(1+6x\right)^2}}}{x^2}\)
\(=\lim\limits_{x\rightarrow0}\left(\frac{-4}{\sqrt{1+4x}+2x+1}+\frac{8x+12}{\left(2x+1\right)^2+\left(2x+1\right)\sqrt[3]{1+6x}+\sqrt[3]{\left(1+6x\right)^2}}\right)=\frac{-4}{1+1}+\frac{12}{1+1+1}=2\)
\(d=\lim\limits_{x\rightarrow0}\frac{\sqrt{1+6x}\left(\sqrt{1+4x}-1\right)}{x}+\lim\limits_{x\rightarrow0}\frac{\sqrt{1+6x}-1}{x}\)
\(=\lim\limits_{x\rightarrow0}\frac{4x\sqrt{1+6x}}{x\left(\sqrt{1+4x}+1\right)}+\lim\limits_{x\rightarrow0}\frac{6x}{x\left(\sqrt{1+6x}+1\right)}\)
\(=\lim\limits_{x\rightarrow0}\frac{4\sqrt{1+6x}}{\sqrt{1+4x}+1}+\lim\limits_{x\rightarrow0}\frac{6}{\sqrt{1+6x}+1}=\frac{4}{1+1}+\frac{6}{1+1}=5\)
\(e=\lim\limits_{x\rightarrow0}\frac{\sqrt[3]{1+4x}\left(\sqrt{1+2x}-1\right)}{x}+\lim\limits_{x\rightarrow0}\frac{\sqrt[3]{1+4x}-1}{x}\)
\(=\lim\limits_{x\rightarrow0}\frac{2x\sqrt[3]{1+4x}}{x\left(\sqrt{1+2x}+1\right)}+\lim\limits_{x\rightarrow0}\frac{4x}{x\left(\sqrt[3]{\left(1+4x\right)^2}+\sqrt[3]{1+4x}+1\right)}\)
\(=\lim\limits_{x\rightarrow0}\frac{2\sqrt[3]{1+4x}}{\sqrt{1+2x}+1}+\lim\limits_{x\rightarrow0}\frac{4}{\sqrt[3]{\left(1+4x\right)^2}+\sqrt[3]{1+4x}+1}=\frac{2}{1+1}+\frac{4}{1+1+1}=\frac{7}{3}\)

a/ \(=lim\frac{3\left(\frac{2}{7}\right)^n-8}{4.\left(\frac{3}{7}\right)^n+5}=-\frac{8}{5}\)
b/ \(=lim\frac{6.4^n-\frac{2}{9}.6^n}{\frac{1}{2}.6^n+4.3^n}=lim\frac{6\left(\frac{4}{6}\right)^n-\frac{2}{9}}{\frac{1}{2}+4.\left(\frac{3}{6}\right)^n}=\frac{-\frac{2}{9}}{\frac{1}{2}}=-\frac{4}{9}\)
c/ \(=lim\frac{\left(-\frac{3}{5}\right)^n+2}{\left(\frac{1}{5}\right)^n-1}=\frac{2}{-1}=-2\)
d/ \(=lim\frac{n\left(n+1\right)}{2\left(n^2+n+1\right)}=lim\frac{1+\frac{1}{n}}{2+\frac{2}{n}+\frac{2}{n^2}}=\frac{1}{2}\)

Giới hạn của dãy nên bạn tự hiểu n tiến tới dương vô cực
1.
\(lim\frac{3n+1}{\sqrt[3]{\left(n^3+3n+1\right)^2}+n\sqrt{n^3+3n+1}+n^2}=lim\frac{3+\frac{1}{n}}{\sqrt[3]{\frac{\left(n^3+3n+1\right)^2}{n^3}}+\sqrt{n^3+3n+1}+n}=\frac{3}{\infty}=0\)
b=\(lim\left(\sqrt[3]{n^3+2n}-n+n-\sqrt{n^2+1}\right)=lim\left(\frac{2n}{\sqrt[3]{\left(n^3+2n\right)^2}+n\sqrt[3]{n^3+2n}+n^2}-\frac{1}{n+\sqrt{n^2+1}}\right)\)
\(=lim\left(\frac{2}{\sqrt[3]{\frac{\left(n^3+2n\right)^2}{n^3}}+\sqrt[3]{n^3+2n}+n}-\frac{1}{n+\sqrt{n^2+1}}\right)=0-0=0\)
c\(=lim\left(\frac{2n^2+n}{\sqrt[3]{\left(n^3+n\right)^2}+\sqrt[3]{\left(n^3+n\right)\left(n^3-2n^2\right)}+\sqrt[3]{\left(n^3-2n^2\right)^2}}\right)\)
\(=lim\left(\frac{2+\frac{1}{n}}{\sqrt[3]{\left(1+\frac{1}{n^2}\right)^2}+\sqrt[3]{\left(1+\frac{1}{n^2}\right)\left(1-\frac{2}{n}\right)}+\sqrt[3]{\left(1-\frac{2}{n}\right)^2}}\right)=\frac{2}{1+1.1+1}=\frac{2}{3}\)
2.
a\(=lim\left[n\left(2-\sqrt{1+\frac{3}{n}}\right)\right]=+\infty\left(2-1\right)=+\infty\)
\(b=lim\left[n\left(\sqrt{1+\frac{2}{n^2}}-\sqrt{\frac{3}{n}+\frac{1}{n^2}}\right)\right]=+\infty\left(1-0\right)=+\infty\)
\(c=lim\left[n^3\left(\frac{sin2n}{n^2}-3\right)\right]=+\infty\left(0-3\right)=-\infty\)

a/ \(=lim\frac{1}{\sqrt{n+1}+\sqrt{n}}=\frac{1}{\infty}=0\)
b/ \(=lim\frac{6n+1}{\sqrt{n^2+5n+1}+\sqrt{n^2-n}}=\frac{6+\frac{1}{n}}{\sqrt{1+\frac{5}{n}+\frac{1}{n^2}}+\sqrt{1-\frac{1}{n}}}=\frac{6}{1+1}=3\)
c/ \(=lim\frac{6n-9}{\sqrt{3n^2+2n-1}+\sqrt{3n^2-4n+8}}=lim\frac{6-\frac{9}{n}}{\sqrt{3+\frac{2}{n}-\frac{1}{n^2}}+\sqrt{3-\frac{4}{n}+\frac{8}{n^2}}}=\frac{6}{\sqrt{3}+\sqrt{3}}=\sqrt{3}\)
d/ \(=lim\frac{\left(\frac{2}{6}\right)^n+1-4\left(\frac{4}{6}\right)^n}{\left(\frac{3}{6}\right)^n+6}=\frac{1}{6}\)
e/ \(=lim\frac{\left(\frac{3}{5}\right)^n-\left(\frac{4}{5}\right)^n+1}{\left(\frac{3}{5}\right)^n+\left(\frac{4}{5}\right)^n-1}=\frac{1}{-1}=-1\)
f/ Ta có công thức:
\(1+3+...+\left(2n+1\right)^2=\left(n+1\right)^2\)
\(\Rightarrow lim\frac{1+3+...+2n+1}{3n^2+4}=lim\frac{\left(n+1\right)^2}{3n^2+4}=lim\frac{\left(1+\frac{1}{n}\right)^2}{3+\frac{4}{n^2}}=\frac{1}{3}\)
g/ \(=lim\left(\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{n}-\frac{1}{n+1}\right)=lim\left(1-\frac{1}{n+1}\right)=1-0=1\)
h/ Ta có: \(1^2+2^2+...+n^2=\frac{n\left(n+1\right)\left(2n+1\right)}{6}\)
\(\Rightarrow lim\frac{n\left(n+1\right)\left(2n+1\right)}{6n\left(n+1\right)\left(n+2\right)}=lim\frac{2n+1}{6n+12}=lim\frac{2+\frac{1}{n}}{6+\frac{12}{n}}=\frac{2}{6}=\frac{1}{3}\)

\(=lim\frac{2.2^{5n}+3}{9.3^{5n}+1}=lim\frac{2.\left(\frac{2}{3}\right)^{5n}+3\left(\frac{1}{3}\right)^{5n}}{9+\left(\frac{1}{3}\right)^{5n}}=\frac{0}{9}=0\)
\(b=lim\frac{\left(-\frac{1}{3}\right)^n+4}{-1\left(-\frac{1}{3}\right)^n-2}=\frac{4}{-2}=-2\)
\(c=1+lim\frac{-n}{n^2+\sqrt{n^4+n}}=1+lim\frac{-\frac{1}{n}}{1+\sqrt{1+\frac{1}{n^3}}}=1+\frac{0}{2}=1\)
\(-2\le2cosn^2\le2\Rightarrow\frac{-2}{n^2+1}\le\frac{2cosn^2}{n^2+1}\le\frac{2}{n^2+1}\)
Mà \(lim\frac{-2}{n^2+1}=lim\frac{2}{n^2+1}=0\Rightarrow lim\frac{2cosn^2}{n^2+1}=0\)
\(d=lim\left[n\left(\sqrt{1-\frac{2}{n^2}}-1+1-\sqrt[3]{1+\frac{2}{n^2}}\right)\right]\)
\(=lim\left[n\left(\frac{-\frac{2}{n^2}}{\sqrt{1-\frac{2}{n^2}}+1}-\frac{\frac{2}{n^2}}{\sqrt[3]{\left(1+\frac{2}{n^2}\right)^2}+\sqrt[3]{1+\frac{2}{n^2}}+1}\right)\right]\)
\(=lim\left(\frac{-\frac{2}{n}}{\sqrt{1-\frac{2}{n^2}}+1}-\frac{\frac{2}{n}}{\sqrt[3]{\left(1+\frac{2}{n^2}\right)^2}+\sqrt[3]{1+\frac{2}{n^2}}+1}\right)=\frac{0}{2}-\frac{0}{1+1+1}=0\)

\(a=lim\frac{n^2+n}{6n^3}=lim\frac{\frac{1}{n}+\frac{1}{n^3}}{6}=\frac{0}{6}=0\)
\(b=lim\frac{1+\frac{2}{n}}{1+\frac{1}{n}}+lim\frac{sinn}{2^n}=1+0=1\)
Giải thích: \(-1\le sin\left(n\right)\le1\) \(\forall n\Rightarrow\frac{-1}{2^n}\le\frac{sin\left(n\right)}{2^n}\le\frac{1}{2^n}\)
Mà \(lim\frac{-1}{2^n}=lim\frac{1}{2^n}=0\Rightarrow lim\frac{sin\left(n\right)}{2^n}=0\) theo nguyên tắc giới hạn kẹp
\(c=lim\frac{-3n-1}{\sqrt{n^2-3n}+\sqrt{n^2+1}}=lim\frac{-3-\frac{1}{n}}{\sqrt{1-\frac{3}{n}}+\sqrt{1+\frac{1}{n^2}}}=\frac{-3}{1+1}=-\frac{3}{2}\)
\(d=lim\frac{3n^2}{\sqrt[3]{\left(n^3+3n^2\right)^2}+n\sqrt[3]{n^3+3n^2}+n^2}=lim\frac{3}{\sqrt[3]{\left(1+\frac{3}{n}\right)^2}+\sqrt[3]{1+\frac{3}{n}}+1}=\frac{3}{1+1+1}=1\)

Bạn muốn tìm giới hạn nhưng lại không chỉ rõ $n$ chạy đến đâu?
Điển hình như câu 1:
$n\to 0$ thì giới hạn là $3$
$n\to \pm \infty$ thì giới hạn là $\pm \infty$
Bạn phải ghi rõ đề ra chứ?