Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Cách 1: Ta có:
y' = 6sin5x.cosx - 6cos5x.sinx + 6sinx.cos3x - 6sin3x.cosx = 6sin3x.cosx(sin2x - 1) + 6sinx.cos3x(1 - cos2x) = - 6sin3x.cos3x + 6sin3x.cos3x = 0.
Vậy y' = 0 với mọi x, tức là y' không phụ thuộc vào x.
Cách 2:
y = sin6x + cos6x + 3sin2x.cos2x(sin2x + cos2x) = sin6x + 3sin4x.cos2x + 3sin2x.cos4x + cos6x = (sin2x + cos2x)3 = 1
Do đó, y' = 0.
b) Cách 1:
Áp dụng công thức tính đạo hàm của hàm số hợp
(cos2u)' = 2cosu(-sinu).u' = -u'.sin2u
Ta được
y' =[sin - sin
] + [sin
- sin
] - 2sin2x = 2cos
.sin(-2x) + 2cos
.sin(-2x) - 2sin2x = sin2x + sin2x - 2sin2x = 0,
vì cos = cos
=
.
Vậy y' = 0 với mọi x, do đó y' không phụ thuộc vào x.
Cách 2: vì côsin của hai cung bù nhau thì đối nhau cho nên
cos2 = cos2
'
cos2 = cos2
.
Do đó
y = 2 cos2 + 2cos2
- 2sin2x = 1 +cos
+ 1 +cos
- (1 - cos2x) = 1 +cos
+ cos
+ cos2x = 1 + 2cos
.cos(-2x) + cos2x = 1 + 2
cos2x + cos2x = 1.
Do đó y' = 0.

\(a,sin2x-2sinx+cosx-1=0\)
\(\Leftrightarrow2sinxcosx-2sinx+cosx-1=0\)
\(\Leftrightarrow2sinx\left(cosx-1\right)+cosx-1=0\)
\(\Leftrightarrow\left(cosx-1\right)\left(2sinx+1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}cosx=1\\sinx=-\frac{1}{2}\end{cases}\Leftrightarrow\orbr{\begin{cases}x=2k\pi\\x=\frac{-\pi}{6}+2k\pi\end{cases}}}\)
\(b,\sqrt{2}\left(sinx-2cosx\right)=2-sin2x\)
\(\Leftrightarrow\sqrt{2}sinx-2\sqrt{2}cosx-2+2sinxcosx=0\)
\(\Leftrightarrow\sqrt{2}sinx\left(1+\sqrt{2}cosx\right)-2.\left(\sqrt{2}cosx+1\right)=0\)
\(\Leftrightarrow\left(\sqrt{2}cosx+1\right)\left(\sqrt{2}sinx-2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}cosx=\frac{-\sqrt{2}}{2}\\sinx=\frac{2\sqrt{2}}{2}\left(l\right)\end{cases}}\)(vì \(-1\le sinx\le1\))
\(\Leftrightarrow\orbr{\begin{cases}x=\frac{3\pi}{4}+2k\pi\\x=\frac{5\pi}{4}+2k\pi\end{cases}}\)
\(c,\frac{1}{cosx}-\frac{1}{sinx}=2\sqrt{2}cos\left(x+\frac{\pi}{4}\right)\)
\(\Leftrightarrow\frac{sinx-cosx}{sinx.cosx}=2\sqrt{2}cos\left(x+\frac{\pi}{4}\right)\)
\(\Leftrightarrow\frac{-\sqrt{2}cos\left(x+\frac{\pi}{4}\right)}{sinx.cosx}=2\sqrt{2}cos\left(x+\frac{\pi}{4}\right)\)
\(\Leftrightarrow sin2x+1=0\)
\(\Leftrightarrow sin2x=-1\)
\(\Leftrightarrow2x=\frac{3\pi}{2}+2k\pi\)
\(\Leftrightarrow x=\frac{3\pi}{4}+k\pi\)

a/ \(\Leftrightarrow2cosx.cos2x=cos2x\)
\(\Leftrightarrow2cosx.cos2x-cos2x=0\)
\(\Leftrightarrow cos2x\left(2cosx-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}cos2x=0\\cosx=\frac{1}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}2x=\frac{\pi}{2}+k\pi\\x=\pm\frac{\pi}{3}+k2\pi\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{4}+\frac{k\pi}{2}\\x=\pm\frac{\pi}{3}+k2\pi\end{matrix}\right.\)
b/ \(\Leftrightarrow2sinx.sin2x=sinx\)
\(\Leftrightarrow2sinx.sin2x-sinx=0\)
\(\Leftrightarrow sinx\left(2sin2x-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}sinx=0\\sin2x=\frac{1}{2}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=k\pi\\2x=\frac{\pi}{6}+k2\pi\\2x=\frac{5\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=k\pi\\x=\frac{\pi}{12}+k\pi\\x=\frac{5\pi}{12}+k\pi\end{matrix}\right.\)
c/ \(\Leftrightarrow sin3x-sinx+sin4x-sin2x=0\)
\(\Leftrightarrow2cos2x.sinx+2cos3x.sinx=0\)
\(\Leftrightarrow sinx\left(cos2x+cos3x\right)=0\)
\(\Leftrightarrow2sinx.2cos\frac{5x}{2}.cos\frac{x}{2}=0\)
\(\Rightarrow\left[{}\begin{matrix}sinx=0\\cos\frac{5x}{2}=0\\cos\frac{x}{2}=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=k\pi\\\frac{5x}{2}=\frac{\pi}{2}+k2\pi\\\frac{x}{2}=\frac{\pi}{2}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=k\pi\\x=\frac{\pi}{5}+\frac{k4\pi}{5}\\x=\pi+k4\pi\end{matrix}\right.\)
d/ \(\Leftrightarrow sin3x-sinx-\left(sin4x-sin2x\right)=0\)
\(\Leftrightarrow2cos2x.sinx-2cos3x.sinx=0\)
\(\Leftrightarrow sinx\left(cos2x-cos3x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\\cos2x=cos3x\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=k\pi\\2x=3x+k2\pi\\2x=-3x+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=k\pi\\x=\frac{k2\pi}{5}\end{matrix}\right.\)
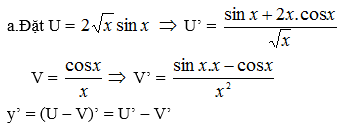
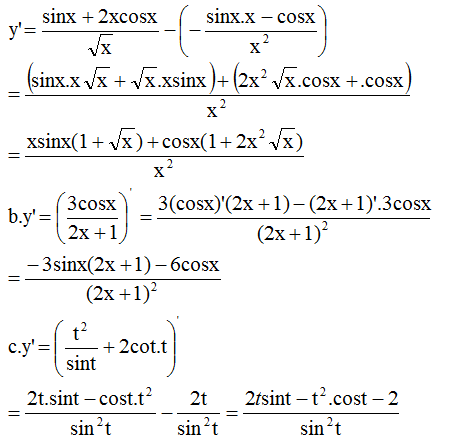
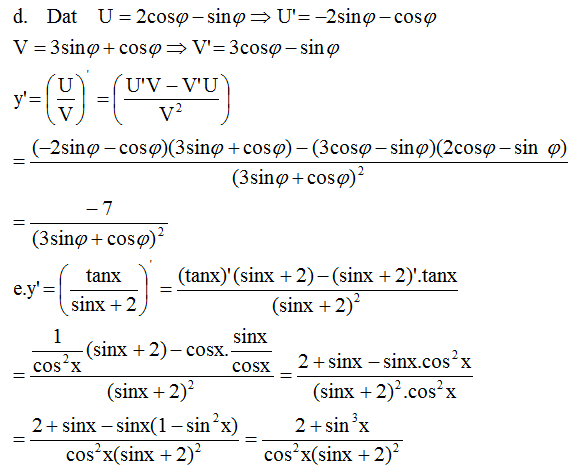


Chọn D
Bước đầu tiên áp dung công thức u α / với u = sin 2 x + 1
Vậy
y ' = sin 3 2 x + 1 / = 3 sin 2 2 x + 1 . sin 2 x + 1 / .
* Tính sin 2 x + 1 / : Áp dụng sin u / , với u = 2 x + 1
Ta được:
sin 2 x + 1 / = cos 2 x + 1 . 2 x + 1 / = 2 cos 2 x + 1 .
⇒ y ' = 3. sin 2 2 x + 1 .2 cos 2 x + 1 = 6 sin 2 2 x + 1 cos 2 x + 1 .