
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


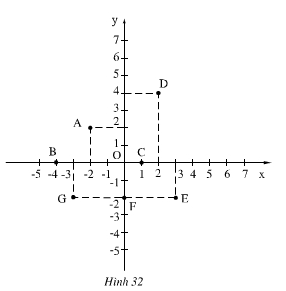
Tọa độ các điểm đó là:
A(-2; 2) ; B(-4; 0)
C(1; 0) ; D(2; 4)
E(3; -2) ; F(0; -2)
G(-3; -2)

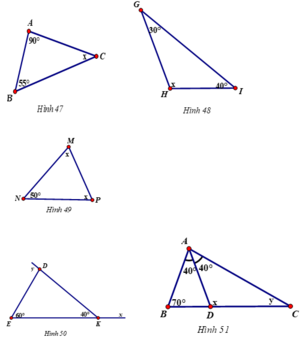
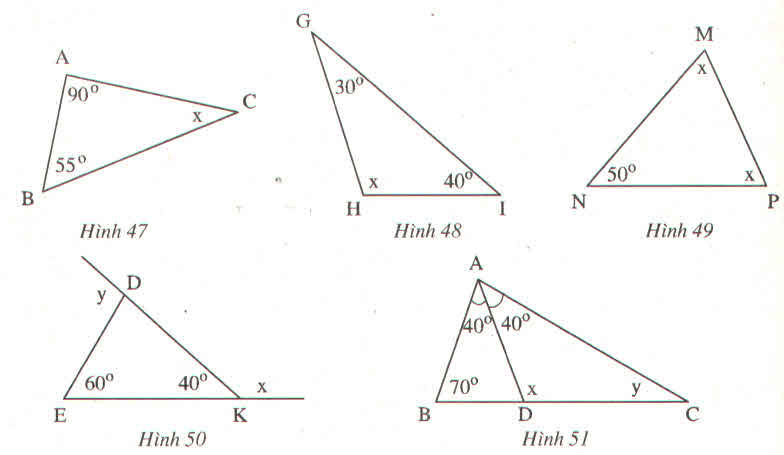
Hình 47:
x+ 900 + 550 = 1800
⇒ x = 1800 – ( 900+ 550)= 350
Hình 48:
x+ 400 + 300 = 1800
⇒ x= 1800 – ( 400+ 390)= 1100
Hình 49:
x+ x + 500= 1800
⇒2x= 1800 – 500 = 1300
⇒ x= 1300 : 2 = 650
Hình 50:
y = 600 + 400= 1000 (Mỗi góc ngoài của một tam giác bằng tổng hai góc không kề với nó)
Ta có: x + 400 = 1800 (kề bù)
⇒x = 1800 – 400 = 1400
Hình 51:
Trong ∆ ABC có
(400+ 400) + 700 + y = 1800
⇒ y + 1500 = 1800
⇒ y = 1800 – 1500= 300
Trong ∆ ACD có:
x + 400 + 300= 1800 ( Góc y = 300 giải được ở trên)
x= 1800 – ( 400+ 300)= 1100

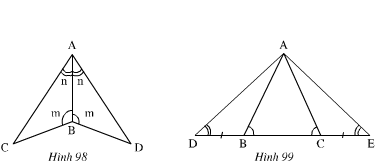
nh 98): Xét ΔABC và ΔABD có:
Nên ΔABC = ΔABD (g.c.g)
- Hình 99): Ta có:
Xét ΔABD và ΔACE có:
Nên ΔABD = ΔACE ( g.c.g)
Xét ΔADC và ΔAEB có:
DC = EB (Vì DC = DB + BC ; EB = EC + BC mà DB = EC)
Nên ΔADC = ΔAEB (g.c.g)
Xem hình 98)
∆ABC và ∆ABD có:
ˆA1A1^=ˆA2A2^(gt)
AB là cạnh chung.
ˆB1B1^=ˆB2B2^(gt)
Nên ∆ABC=∆ABD(g.c.g)
Xem hình 99)
Ta có:
ˆB1B1^+ˆB2B2^=1800 (Hai góc kề bù).
ˆC1C1^+ ˆC2C2^=1800 (Hai góc kề bù)
Mà ˆB2B2^=ˆC2C2^(gt)
Nên ˆB1B1^=ˆC1C1^
* ∆ABD và ∆ACE có:
ˆB1B1^=ˆC1C1^(cmt)
BD=EC(gt)
ˆDD^ = ˆEE^(gt)
Nên ∆ABD=∆ACE(g.c.g)
* ∆ADC và ∆AEB có:
ˆDD^=ˆEE^(gt)
ˆC2C2^=ˆB2B2^(gt)
DC=EB
Nên ∆ADC=∆AEB(g.c.g)



Cái bài này mình đã từng đăng để hỏi mấy bạn kia.
Nhưng đề câu này thiểu bạn ơi.
Phải có x=a/m ; y=b/m
À thôi, mk viết đầy đủ đề thử nhé !
Giả sử:x=a/m;y=b/m (a,b,m thuộc Z.m > 0) và x < y.
Hãy chứng minh (chứng tỏ) rằng nếu chọn z=a+b/2m thì ta có x < y < z.
Trong sách lớp 7 đề y như z đó !
Mk ghi cách làm luôn nha !
Giả sử x=a/m,y=b/m (a,b,m thuộc Z,m > 0 )
Vì x < y nên ta suy ra a < b.
ta có: x=a/m, y=b/m <=> x=2a/am. y=2b/2m
mà a < b nên a+a < a+b <=> 2a < a+b
Do 2a < a+b thì x < y ( 1 )
Ta lại có: a < b nên a+b < b+b <=> a+b < 2b
Mà a+b < 2b <=> x < z ( 2 )
Từ ( 1 ) và ( 2 ) suy ra x < y < z (ĐPCM)

\(a.\sqrt{0,01}-\sqrt{0,25}=\sqrt{0.1^2}-\sqrt{0,5^2}\)
\(=|0.1|-|0,5|=0,1-0,5=-0,4\)
\(\sqrt{0,01}-\sqrt{0,25}\)
\(=\sqrt{\frac{1}{100}}-\sqrt{\frac{25}{100}}\)
\(=\frac{1}{10}-\frac{5}{10}\)
\(=\frac{-2}{5}\)
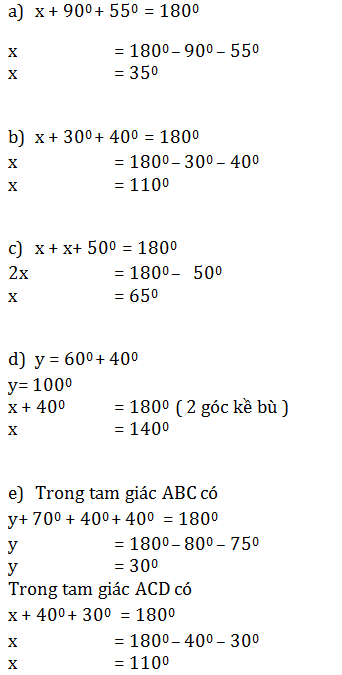
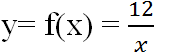






 (a, b, m ∈ Z; m > 0) và x < y. Hãy chứng minh nếu chọn
(a, b, m ∈ Z; m > 0) và x < y. Hãy chứng minh nếu chọn 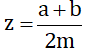 thì ta có x < z < y.
thì ta có x < z < y.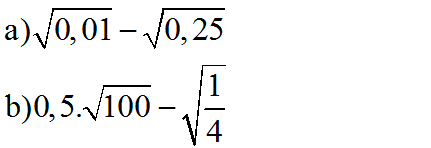
Áp dụng định lý tổng ba góc trong một tam giác bằng 180º ta có:
- Hình 47
x + 90o + 55o = 180o
x = 180o - 90o - 55o
x = 35o
- Hình 48
x + 30o + 40o = 180o
x = 180o - 30o - 40o
x = 110o
- Hình 49
x + x + 50o = 180o
2x = 180o - 50o
x = 65o
Áp dụng định lý góc ngoài của tam giác ta có:
- Hình 50
y = 60o + 40o
y = 100o
x + 40o = 180o (2 góc kề bù)
x = 140o
- Hình 51
Áp dụng định lý góc ngoài trong tam giác ABD có: x = 70º + 40º = 110º
Áp dụng định lý tổng ba góc trong tam giác ADC có:
y + 110º + 40º = 180º ⇒ y = 30º.