
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Giá trị của biểu thức không âm khi :
\(2x-5\ge0\Leftrightarrow2x\ge5\)
\(\Leftrightarrow\) \(x\ge\dfrac{5}{2}\)
Vậy để 2x-5 không âm khi \(x\ge\dfrac{5}{2}\)
b) Giá trị của biểu thức -3xkhông lớn hơn giá trị của biểu thức -7x + 5 khi: \(-3x\le-7x+5\)
\(\Leftrightarrow\) \(-3x+7x\le5\Leftrightarrow4x\le5\Leftrightarrow x\le\dfrac{5}{4}\)
Vậy để giá trị của -3x không lớn hơn giá trị của -7x+5 thì \(x\le\dfrac{5}{4}\)
a)Ta có bất phương trình: 2x – 5 ≥ 0 ⇔ 2x > 5
⇔x≥52x≥52
Vậy để cho 2x – 5 không âm thì x≥52x≥52 .
b)Tìm x sao cho giá trị của biểu thức -3x không lớn hơn giá trị của biểu thức -7x + 5.
Ta có : -3x ≤ -7x + 5 ⇔-3x + 7x ≤ 5
⇔2x ≤ 5
⇔x ≤5252
Vậy để cho giá trị của -3x không lớn hơn giá trị của -7x + 5 thì x≤52x≤52 .

A/ Theo đề ta có \(\frac{x}{2}-\frac{x-5}{10}\) không âm
\(\Rightarrow\frac{x}{2}-\frac{x-5}{10}\ge0\)
\(\Rightarrow\frac{5x}{10}-\frac{x-5}{10}\ge0\)
\(\Rightarrow\frac{5x-x+5}{10}\ge0\)
\(\Rightarrow\frac{4x+5}{10}\ge0\)
\(\Rightarrow4x+5\ge0\)
\(\Rightarrow4x\ge-5\)
\(\Rightarrow x\ge-\frac{5}{4}\)
\(\Rightarrow S=\left\{x\in R;x\ge-\frac{5}{4}\right\}\)
B/ theo đề ta có \(\frac{2x-3}{8}-\frac{x-5}{12}\) không dương
\(\Rightarrow\frac{2x-3}{8}-\frac{x-5}{12}\le0\)
\(\Rightarrow\frac{3\left(2x-3\right)}{24}-\frac{2\left(x-5\right)}{24}\le0\)
\(\Rightarrow\frac{6x-9}{24}-\frac{2x-10}{24}\le0\)
\(\Rightarrow\frac{6x-9-2x+10}{24}\le0\)
\(\Rightarrow\frac{4x-1}{24}\le0\)
\(\Rightarrow4x-1\le0\)
\(\Rightarrow4x\le1\)
\(\Rightarrow x\le\frac{1}{4}\)
\(\Rightarrow S=\left\{x\in R;x\le\frac{1}{4}\right\}\)

a) Để giá trị biểu thức 5 – 2x là số dương
<=> 5 – 2x > 0
<=> -2x > -5 ( Chuyển vế và đổi dấu hạng tử 5 )
\(\Leftrightarrow x< \frac{5}{2}\)( Chia cả 2 vế cho -2 < 0 ; BPT đổi chiều )
Vậy : \(x< \frac{5}{2}\)
b) Để giá trị của biểu thức x + 3 nhỏ hơn giá trị biểu thức 4x - 5 thì:
x + 3 < 4x – 5
<=< x – 4x < -3 – 5 ( chuyển vế và đổi dấu các hạng tử 4x và 3 )
<=> -3x < -8
\(\Leftrightarrow x>\frac{8}{3}\)( Chia cả hai vế cho -3 < 0, BPT đổi chiều).
Vậy : \(x>\frac{8}{3}\)
c) Để giá trị của biểu thức 2x +1 không nhỏ hơn giá trị của biểu thức x + 3 thì:
2x + 1 ≥ x + 3
<=> 2x – x ≥ 3 – 1 (chuyển vế và đổi dấu các hạng tử 1 và x).
<=> x ≥ 2.
Vậy x ≥ 2.
d) Để giá trị của biểu thức x2 + 1 không lớn hơn giá trị của biểu thức (x - 2)2 thì:
x2 + 1 ≤ (x – 2)2
<=> x2 + 1 ≤ x2 – 4x + 4
<=> x2 – x2 + 4x ≤ 4 – 1 ( chuyển vế và đổi dấu hạng tử 1; x2 và – 4x).
<=> 4x ≤ 3
\(\Leftrightarrow x\le\frac{3}{4}\)( Chia cả 2 vế cho 4 > 0 )
Vậy : \(x\le\frac{3}{4}\)

a/ A = \(2x-5\ge0\)
\(\Leftrightarrow\)\(2x\ge5\)
\(\Leftrightarrow\)\(x\ge\frac{5}{2}\)
b/ \(\frac{4x-1}{3}\)- \(\frac{2-x}{15}\)\(\le\)\(\frac{10x-3}{5}\)
\(\Leftrightarrow\)5(4x + 1) - 2 - x \(\le\)3(10x - 3)
\(\Leftrightarrow\)20x + 5 - 2 -x \(\le\)30x - 9
\(\Leftrightarrow\)9x - 30x \(\le\)-9 + 2
\(\Leftrightarrow\)-21x \(\le\)-7
\(\Leftrightarrow\)x \(\ge\)\(\frac{1}{3}\)
Kết luận và biểu diễn tập nghiệm nha

Bài 1:
a) Vì giá trị của biểu thức \(\frac{3x-2}{4}\) không nhỏ hơn giá trị của biểu thức \(\frac{3x+3}{6}\) nên \(\frac{3x-2}{4}\) \(\ge\) \(\frac{3x+3}{6}\)
TH1: \(\frac{3x-2}{4}\) = \(\frac{3x+3}{6}\)
=> (3x-2)6 = (3x+3)4
18x -12= 12x+12
=> x = 4
TH2: \(\frac{3x-2}{4}\) > \(\frac{3x+3}{6}\)
=> (3x-2)6 > (3x+3)4
18x-12> 12x+12
=> x \(\ge\) 5
b) Vì ( x+1)2 \(\ge\) 0; (x-1)2 \(\ge\) 0 mà (x+1) luôn lớn hơn (x-1) với mọi x nên không có giá trị của x thỏa mãn (x+1)2 nhỏ hơn (x-1)2
c) Phần c bạn cũng xét tương tự như phần a
TH1: \(\frac{2x-3}{35}+\frac{x\left(x-2\right)}{7}=\frac{x^2}{7}-\frac{2x-3}{5}\)
TH2: \(\frac{2x-3}{35}+\frac{x\left(x-2\right)}{7}<\frac{x^2}{7}-\frac{2x-3}{5}\)

\(\frac{x^2+2x}{2x+10}+\frac{x-5}{x}+\frac{50-5x}{2x\left(x+5\right)}=\frac{x^2+2x}{2\left(x+5\right)}+\frac{x-5}{x}+\frac{50-5x}{2x\left(x+5\right)}=\)
\(=\frac{x\left(x^2+2x\right)+2\left(x+5\right)\left(x-5\right)+50-5x}{2x\left(x+5\right)}=\frac{x^3+2x^2+2x^2-50+50-5x}{2x\left(x+5\right)}=\frac{x^3+4x^2-5x}{2x\left(x+5\right)}=\)
\(=\frac{x\left(x^2+4x-5\right)}{2x\left(x+5\right)}=\frac{x\left(x^2+4x-5\right)}{2x\left(x+5\right)}=\frac{x\left(x^2-1+4\left(x-1\right)\right)}{2x\left(x+5\right)}=\frac{x\left(x-1\right)\left(x+5\right)}{2x\left(x+5\right)}\)
a/ Để biểu thức xác đinh => 2x(x+5) khác 0 => x khác 0 và x khác -5
b/ Gọi biểu thức là A. Rút gọn A ta được:
\(A=\frac{x\left(x-1\right)\left(x+5\right)}{2x\left(x+5\right)}=\frac{x-1}{2}\left(x\ne0;x\ne-5\right)\)
A=1 => x-1=2 => x=3
c/ A=-1/2 <=> x-1=-1 => x=0
d/ A=-3 <=> x-1=-6 => x=-5

a, Vì \(2+\frac{3-2x}{5}\)không nhỏ hơn \(\frac{x+3}{4}-x\)
\(\Rightarrow2+\frac{3-2x}{5}\ge\frac{x+3}{4}-x\)
Giải phương trình :
\(2+\frac{3-2x}{5}\ge\frac{x+3}{4}-x\)
\(\Rightarrow\frac{40}{20}+\frac{4\left(3-2x\right)}{20}\ge\frac{5\left(x-3\right)}{20}-\frac{20x}{20}\)
\(\Rightarrow40+12-8x\ge5x-15-20x\)
\(\Rightarrow7x=67\)
\(\Rightarrow x\ge\frac{67}{7}\)
b, \(\frac{2x+1}{6}-\frac{x-2}{9}>-3\)
\(\Rightarrow\frac{3\left(2x+1\right)}{18}-\frac{2\left(x-2\right)}{18}>\frac{-54}{18}\)
\(\Rightarrow6x+3-2x+4>-54\)
\(\Rightarrow4x>-61\)
\(\Rightarrow x>\frac{-61}{4}\)\(\left(1\right)\)
Và : \(x-\frac{x-3}{4}\ge3-\frac{x-3}{12}\)
\(\frac{12x}{12}-\frac{3\left(x-3\right)}{12}\ge\frac{36}{12}-\frac{x-3}{12}\)
\(\Rightarrow12x-3x+9\ge36-x+3\)
\(\Rightarrow10x\ge30\)
\(\Rightarrow x\ge3\)\(\left(2\right)\)
Từ \(\left(1\right)\)và \(\left(2\right)\)\(\Rightarrow\hept{\begin{cases}x>\frac{-61}{4}\\x\ge3\end{cases}\Rightarrow x>3}\)
Vậy với giá trị x > 3 thì x là nghiệm chung của cả 2 bất phương trình

Để giá trị biểu thức 2x – 5 không âm
⇔ 2x – 5 ≥ 0.
⇔ 2x ≥ 5 (Chuyển vế và đổi dấu hạng tử -5).
⇔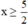 (Chia cả hai vế cho 2 > 0, BPT không đổi chiều).
(Chia cả hai vế cho 2 > 0, BPT không đổi chiều).
Vậy với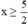 thì giá trị biểu thức 2x – 5 không âm.
thì giá trị biểu thức 2x – 5 không âm.