Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Do mẫu có bậc 2 còn tử bậc 1 \(\Rightarrow\)hàm không có tiệm cận đứng khi và chỉ khi phương trình \(x^2-2mx+1=0\) vô nghiệm
\(\Leftrightarrow\Delta'=m^2-1< 0\)
\(\Rightarrow-1< m< 1\)
Hàm có tiệm cận đứng khi và chỉ khi \(x^2-mx-2m^2=0\) vô nghiệm hoặc không có nghiệm \(x=2\)
\(\Rightarrow\left[{}\begin{matrix}\Delta=m^2+8m^2< 0\\4-2m-2m^2\ne0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m\ne1\\m\ne-2\end{matrix}\right.\)
Với \(m=0\) ko thỏa mãn
Với \(m\ne0\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{x+1}{\sqrt{mx^2+1}}=-\dfrac{1}{\sqrt{m}}\); \(\lim\limits_{x\rightarrow+\infty}\dfrac{x+1}{\sqrt{mx^2+1}}=\dfrac{1}{\sqrt{m}}\)
\(\Rightarrow\) Hàm có 2 TCN khi \(\sqrt{m}\) xác định \(\Rightarrow m>0\)
\(m=0\) hàm số không xác định
\(\lim\limits_{x\rightarrow-\infty}y=\lim\limits_{x\rightarrow-\infty}\dfrac{x+1}{\sqrt{m^2x^2+m-1}}=\lim\limits_{x\rightarrow-\infty}\dfrac{1+\dfrac{1}{x}}{-\sqrt{m^2+\dfrac{m-1}{x^2}}}=\dfrac{-1}{\left|m\right|}\)
\(\)\(\lim\limits_{x\rightarrow+\infty}\dfrac{x+1}{\sqrt{m^2x^2+m-1}}=\lim\limits_{x\rightarrow+\infty}\dfrac{1+\dfrac{1}{x}}{\sqrt{m^2-\dfrac{m-1}{x^2}}}=\dfrac{1}{\left|m\right|}\)
\(\Rightarrow\) đồ thị hàm số luôn có 2 tiệm cận ngang
Để đồ thị hàm số có 4 tiệm cận thì cần có thêm 2 tiệm cận đứng
\(\Rightarrow m^2x^2+m-1=0\) có 2 nghiệm phân biệt
\(\Rightarrow x^2=\dfrac{1-m}{m^2}\) . Do \(x^2>0\Rightarrow1-m>0\Rightarrow m< 1\)
Vậy \(\left\{{}\begin{matrix}m< 1\\m\ne0\end{matrix}\right.\) thì đồ thị hàm số có 4 tiệm cận
Lời giải:
Để đồ thị hàm số có hai tiệm cận đứng thì phương trình $x^2-mx+1=0$ phải có hai nghiệm phân biệt khác $2$, tức là:
\(\left\{\begin{matrix} \Delta=m^2-4>0\\ f(2)=5-2m\neq 0\end{matrix}\right.\)\(\Rightarrow \begin{bmatrix} m>2\\ m<-2\end{bmatrix}\) và $m\neq\frac{5}{2}$
Lời giải:
Bài 1:
Để ĐTHS \(y=\frac{ax+2}{x-b}\) có tiệm cận ngang \(y=2\) thì cần \(a=2\)
Khi đó \(y=\frac{2x+2}{x-b}\) \(\)
Vì ĐTHS đi qua điểm \(M(2,2)\Rightarrow 2=\frac{4+2}{2-b}\Rightarrow b=-1\)
Ta có \(y=\frac{2x+2}{x+1}=2\) (thỏa mãn đkđb)
Vậy \(a=2,b=-1\)
Bài 2:
Dựa vào định nghĩa , nếu \(\lim_{x\rightarrow \infty}y=t\) thì \(y=t\) là tiệm cận ngang của ĐTHS ($x$ tiến đến âm, dương vô cùng)
Như vậy:
Nếu \(m>0\) thì hàm số xác định với mọi \(x\in\mathbb{R}\), khi đó \(\frac{1}{\sqrt{m}}\) chính là TCN của ĐTHS
Nếu \(m=0\Rightarrow y=x+1\) là hàm đa thức hiển nhiên không có TCN
Nếu \(m<0\) thì hàm số xác định chỉ trong một khoảng nào đó của $x$, khi đó ĐTHS hiển nhiên không có TCN.
Vậy \(m\leq 0\)
TH1 : Phương trình x3-3x2-m=0 có một nghiệm đơn x= -1 và một nghiệm kép.
Phương trình x3-3x2-m=0 có nghiệm x=-1 nên (-1)3-3(-1)2-m=0 hay m = -4.
Với m= -4 phương trình trở thành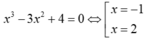 
(thỏa mãn vì x=2 là nghiệm kép).
TH2: Phương trình x3-3x2-m=0 có đúng một nghiệm khác -1 hay x3-3x2=m có một nghiệm khác -1
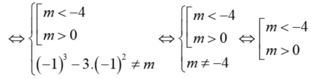
Vậy với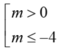 
thỏa mãn yêu cầu đề bài.
Chọn C.
TH1 : Phương trình x3- 3x2-m=0 có một nghiệm đơn x= -1 và một nghiệm kép.
Phương trình x3- 3x2-m=0 có nghiệm x= -1 nên ( -1) 3-3( -1) 2-m=0 hay m= -4.
Với m= -4 phương trình trở thành
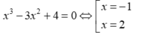
(thỏa mãn vì x= 2 là nghiệm kép).
TH2: Phương trình x3- 3x2-m=0 có đúng một nghiệm khác – 1 hay x3- 3x2= m có một nghiệm khác -1
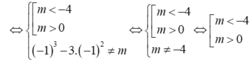
Vậy với m> 0 hoặc m≤ - 4 thỏa mãn yêu cầu đề bài.
Chọn C.
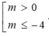
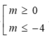
ĐKXĐ: \(x\le1\)
Hàm có tiệm cận đứng khi và chỉ khi phương trình:
\(x-m=0\) có nghiệm \(x< 1\)
\(\Leftrightarrow m< 1\)