Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án D.

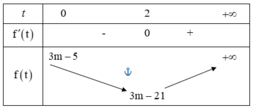
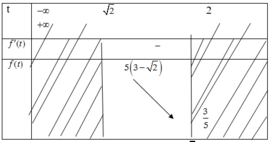
Từ bảng biến thiên trên, ta có bất phương trình đã cho có nghiệm khi và chỉ khi bất phương trình f(t) < 0
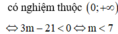

Đáp án B
Điều kiện x + 5 ≥ 0 4 − x ≥ 0 ⇔ − 5 ≤ x ≤ 4
Xét hàm số f x = x + 5 + 4 − x ; x ∈ − 5 ; 4
Ta có:
f ' x = 1 2 x + 5 − 1 2 4 − x ; f ' x = 0 ⇔ 4 − x = x + 5 ⇔ x = − 1 2
Tính các giá trị f − 5 = 3 ; f 4 = 3 ; f − 1 2 = 3 2
⇒ max − 5 ; 4 f x = f − 1 2 = 3 2
Vậy để phương trình m ≤ f x có nghiệm m ≤ max − 5 ; 4 f x ⇔ m ≤ 3 2

Đáp án C.
Ta có:
cos π 4 = 1 + 2 2 m − 1 3 1 + 2 m − 1 2 = 1 2 ⇔ 9 4 m 2 − 4 m + 2 = 2 4 m − 1 2 ⇔ 4 m 2 − 20 m + 16 = 0 ⇔ m = 1 m = 4
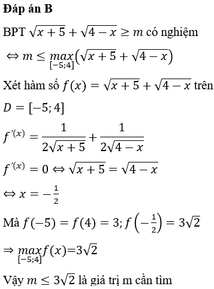

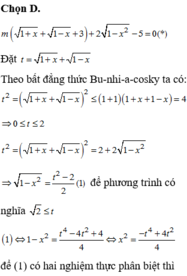

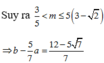


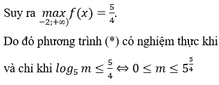
Đáp án A
Điều kiện x ≥ − 2
Đặt t = x + 2 t ≥ 0 ⇒ x = t 2 − 2
Khi đó phương trình tương đương
5 − t 2 + t + 2 − 5 m = 0 ⇔ m = 5 − t 2 + t + 1
Xét hàm số f t = 5 − t 2 + t + 1 ; t ≥ 0.
Ta có:
f ' t = − 2 t + 1 5 − t 2 + t + 1 ; f ' t = 0 ⇔ t = 1 2
Từ bảng biến thiên ra suy ra phương trình có nghiệm thì 0 < m ≤ 5 5 4