
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

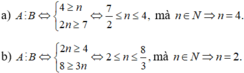

Bài 1:
Ta có: \(9(x-1)^2-4(2x+3)^2=(3x-3)^2-(4x+6)^2\)
\(=(3x-3-4x-6)(3x-3+4x+6)=-(x+9)(7x+3)\)
Bài 2:
Có: \(x^2-x+\frac{9}{20}=x^2-2x.\frac{1}{2}+\frac{1}{4}+\frac{1}{5}=\left(x-\frac{1}{2}\right)^2+\frac{1}{5}\)
Ta thấy \(\left(x-\frac{1}{2}\right)^2\geq 0\forall x\in\mathbb{R}\Rightarrow x^2-x+\frac{9}{20}\geq \frac{1}{5}>0\forall x\in\mathbb{R}\)
Ta có đpcm.
Bài 3:
Thực hiện phân tích:
\(f(x)=x^3-8x^2+ax-5=x(x^2-3x+1)-5(x^2-3x+1)+ax-16x\)
\(=(x-5)(x^2-3x+1)+ax-16x\)
Thấy rằng bậc của \(ax-16x\) nhỏ hơn bậc của $g(x)$ nên $ax-16x$ là dư của $f(x)$ cho $g(x)$
Để \(f(x)\vdots g(x)\Rightarrow ax-16x=0\forall x\Rightarrow a=16\)
Bài 4:
Để \(\overline{2017x}\vdots 12\Leftrightarrow \left\{\begin{matrix} \overline{2017x}\vdots 3(1)\\ \overline{2017x}\vdots 4(2)\end{matrix}\right.\)
\((1)\Leftrightarrow 2+0+1+7+x\vdots 3\Leftrightarrow 10+x\vdots 3\Leftrightarrow x+1\vdots 3\)
\((2)\Leftrightarrow \overline{7x}\vdots 4\Rightarrow x\in\left\{2;6\right\}\)
Từ hai điều trên suy ra \(x=2\)
Bài 5:
Ta có: \(x+\frac{1}{x}=\sqrt{2017}\Rightarrow \left(x+\frac{1}{x}\right)^2=2017\Leftrightarrow x^2+\frac{1}{x^2}+2=2017\)
\(\Leftrightarrow x^2+\frac{1}{x^2}=2015\)
Như vậy: \(A=3x^2-5+\frac{3}{x^2}=3\left(x^2+\frac{1}{x^2}\right)-5=3.2015-5=6040\)
Bài 6:
Đặt \(\left\{\begin{matrix} x+y+z=a\\ xy+yz+xz=b\end{matrix}\right.\). ĐKĐB tương đương với:
\(\left\{\begin{matrix} a^2-2b=3\\ a+b=6\rightarrow b=6-a\end{matrix}\right.\)
\(\Rightarrow a^2-2(6-a)=3\Leftrightarrow a^2-2a+15=0\Leftrightarrow (a+5)(a-3)=0\Leftrightarrow a=3\)
(do \(a\in\mathbb{R}^+\))
Kéo theo \(b=6-a=3\Rightarrow x^2+y^2+z^2=xy+yz+xz\)
Theo BĐT AM-GM thì \(x^2+y^2+z^2\geq xy+yz+xz\)
Dấu bằng xảy ra khi \(x=y=z\Rightarrow x=y=z=1\) do \(x+y+z=3\)

a) Thực hiện phép chia đa thức cho đa thức bth
Được dư cuối là 3
Vậy để f(x) chia hết cho g(x) thì \(3⋮x^2+x+1\)
\(\Rightarrow x^2+x+1\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\) Do \(x^2+x+1>0\)
Ta có bảng :
| \(x^2+x+1\) | \(x\) | Kết luận |
| 1 | 0 hoặc -1 | Nhận |
| 3 | 1 hoặc -2 | Nhận |
Vậy \(x\in\left\{0;1;-1;-2\right\}\) thì \(f\left(x\right)⋮g\left(x\right)\)
b)Ta có : f(x)=(x+2)(x+4)(x+6)(x+8)+2020
=(x+2)(x+8)(x+4)(x+6)+2020
=(x2+10x+16)(x2+10x+24)+2020
Đặt a=x2+10x+16
=> f(x)=a(a+8)+2020
=a2+8a+2020 = a2+3a+5a+15+2005
=a(a+3)+5(a+3)+2005=(a+5)(a+3) +2005
Thay ngược lại ta có : f(x)= (x2+10x+21)(x2+10x+19)+2005
Vì (x2+10x+21)(x2+10x+19) \(⋮\) (x2+10x+21)
=> (x2+10x+21)(x2+10x+19)+2005:(x2+10x+21) dư 2005
Vậy f(x) chia g(x) dư 2005

1.
a)
\(5x\left(x-2y\right)+2\left(2y-x\right)^2\\ =5x\left(x-2y\right)+2\left(x-2y\right)^2\\ =\left(x-2y\right)\left[5x+2\left(x-2y\right)\right]\\ =\left(x-2y\right)\left(5x+2x-4y\right)\\ =\left(x-2y\right)\left(7x-4y\right)\)
b)
\(7x\left(y-4\right)^2-\left(4-y\right)^3\\ =7x\left(4-y\right)^2-\left(4-y\right)^3\\ =\left(4-y\right)^2\left(7x+y-4\right)\)
c)
\(\left(4x-8\right)\left(x^2+6\right)-\left(4x-8\right)\left(x+7\right)+9\left(8-4x\right)\\ =\left(4x-8\right)\left(x^2+6\right)-\left(4x-8\right)\left(x+7\right)-9\left(4x-8\right)\\ =\left(4x-8\right)\left(x^2+6-x-7-9\right)\\ =4\left(x-2\right)\left(x^2-x-10\right)\)

1, a, = (3x+15-x+7 )( 3x+15+x-7)
= ( 2x +22)( 4x+8)
=8( x+11)( x+2)
b, = ( 5x-5y-4x - 4y)(5x-5y+4x+4y)
=(x-9y)(x-y)
2.a,ta có : (n+6)2- (n-6)2 = (n+6-n+6)( n+6+n-6) = 12.2n=24n chia hết cho 24 ( vì 24 chia hết cho 24) (ĐPCM)
b,
Ta có: n^3+3.n^2-n-3=n^2.(n+3) -(n+3)=(n+3).(n-1).(n+1).
-Do n là số lẻ nên đặt n=2k+1.(k thuộc N).
=> n^3+3.n^2-n-3= (2k+4).2k.(2k+2)= 8.k.(k+1).(k+2).
-Do k(k+1) là tích 2 số tự nhiên liên tiếp nên k(k+1) chia hết cho 2 và k(k+1)(k+2) là tích 3 số tự nhiên liên tiếp nên k(k+1)(k+2) chia hết cho 3.
=> 8k(k+1)(k+2) chia hết cho 16 và chia hết cho 3. Mà (16,3)=1.
=> 8k(k+1)(k+2) chia hết cho 16.3.
=> n^3+3.n^2-n-3 chia hết cho 48 với mọi n là số tự nhiên lẻ (đpcm).

Bài 3:
a) ta có: \(A=x^2+4x+9\)
\(=x^2+4x+4+5=\left(x+2\right)^2+5\)
Ta có: \(\left(x+2\right)^2\ge0\forall x\)
\(\Rightarrow\left(x+2\right)^2+5\ge5\forall x\)
Dấu '=' xảy ra khi
\(\left(x+2\right)^2=0\Leftrightarrow x+2=0\Leftrightarrow x=-2\)
Vậy: GTNN của đa thức \(A=x^2+4x+9\) là 5 khi x=-2
b) Ta có: \(B=2x^2-20x+53\)
\(=2\left(x^2-10x+\frac{53}{2}\right)\)
\(=2\left(x^2-10x+25+\frac{3}{2}\right)\)
\(=2\left[\left(x-5\right)^2+\frac{3}{2}\right]\)
\(=2\left(x-5\right)^2+2\cdot\frac{3}{2}\)
\(=2\left(x-5\right)^2+3\)
Ta có: \(\left(x-5\right)^2\ge0\forall x\)
\(\Rightarrow2\left(x-5\right)^2\ge0\forall x\)
\(\Rightarrow2\left(x-5\right)^2+3\ge3\forall x\)
Dấu '=' xảy ra khi
\(2\left(x-5\right)^2=0\Leftrightarrow\left(x-5\right)^2=0\Leftrightarrow x-5=0\Leftrightarrow x=5\)
Vậy: GTNN của đa thức \(B=2x^2-20x+53\) là 3 khi x=5
c) Ta có : \(M=1+6x-x^2\)
\(=-x^2+6x+1\)
\(=-\left(x^2-6x-1\right)\)
\(=-\left(x^2-6x+9-10\right)\)
\(=-\left[\left(x-3\right)^2-10\right]\)
\(=-\left(x-3\right)^2+10\)
Ta có: \(\left(x-3\right)^2\ge0\forall x\)
\(\Rightarrow-\left(x-3\right)^2\le0\forall x\)
\(\Rightarrow-\left(x-3\right)^2+10\le10\forall x\)
Dấu '=' xảy ra khi
\(-\left(x-3\right)^2=0\Leftrightarrow\left(x-3\right)^2=0\Leftrightarrow x-3=0\Leftrightarrow x=3\)
Vậy: GTLN của đa thức \(M=1+6x-x^2\) là 10 khi x=3
Bài 2:
a) \(\left(x+y\right)^2+\left(x^2-y^2\right)\)
\(=\left(x+y\right)^2+\left(x-y\right).\left(x+y\right)\)
\(=\left(x+y\right).\left(x+y+x-y\right)\)
\(=\left(x+y\right).2x\)
c) \(x^2-2xy+y^2-z^2+2zt-t^2\)
\(=\left(x^2-2xy+y^2\right)-\left(z^2-2zt+t^2\right)\)
\(=\left(x-y\right)^2-\left(z-t\right)^2\)
\(=\left[x-y-\left(z-t\right)\right].\left(x-y+z-t\right)\)
\(=\left(x-y-z+t\right).\left(x-y+z-t\right)\)
Chúc bạn học tốt!