
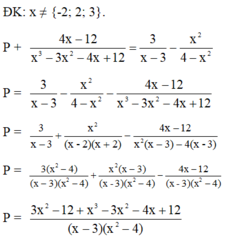
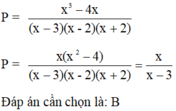
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

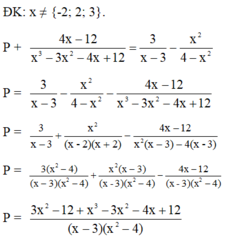
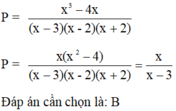

a) 5.(x^2-3x+1)+x.(1-5x)=x-2
\(\Leftrightarrow5x^2-15x+5+x-5x^2=x-2\)
\(\Leftrightarrow-14x-x=-2-5\)
\(\Leftrightarrow-15x=-7\)
\(\Leftrightarrow x=\frac{7}{15}\)
b\(,3x.\left(\frac{4}{3}+1\right)-4x\left(x-2\right)=10\)
\(\Leftrightarrow4x+3x-4x^2+8x-10=0\)
\(\Leftrightarrow-4x^2+15x-10=0\)
Đề sai???
\(c,12x^2-4x\left(3x-5\right)=10x-17\)
\(\Leftrightarrow12x^2-12x^2+20x-10x=-17\)
\(\Leftrightarrow10x=-17\)
\(\Leftrightarrow x=-\frac{17}{10}\)
\(d,4x\left(x-5\right)-7x\left(x-4\right)+3x^2=12\)
\(\Leftrightarrow4x^2-20x-7x^2+28x+3x^2=12\)
\(\Leftrightarrow8x=12\)
\(\Leftrightarrow x=\frac{3}{2}\)

a: \(\Leftrightarrow4\left(x^2+60+17x\right)\left(x^2+60+16x\right)=3x^2\)
\(\Leftrightarrow4\cdot\left[\left(x^2+60\right)^2+33x\left(x^2+60\right)+272x^2\right]=3x^2\)
=>4(x^2+60)^2+132x(x^2+60)+1085x^2=0
=>4(x^2+60)^2+62x(x^2+60)+70x(x^2+60)+1085x^2=0
=>2(x^2+60)(2x^2+120+31x)+35x(2x^2+120+31x)=0
=>(2x^2+120+35x)(2x^2+31x+120)=0
=>\(x\in\left\{\dfrac{-35\pm\sqrt{265}}{4};-\dfrac{15}{2};-8\right\}\)
b: Đặt x^2-3x=a
Phương trình sẽ là \(\dfrac{1}{a+3}+\dfrac{2}{a+4}=\dfrac{6}{a+5}\)
\(\Leftrightarrow\dfrac{a+4+2a+6}{\left(a+3\right)\left(a+4\right)}=\dfrac{6}{a+5}\)
=>(3a+10)(a+5)=6(a^2+7a+12)
=>6a^2+42a+72=3a^2+15a+10a+50
=>3a^2+17a+22=0
=>x=-2 hoặc x=-11/3

Bài 1.
1) ( 2x + 1 )3 - ( 2x + 1 )( 4x2 - 2x + 1 ) - 3( 2x - 1 ) = 15
<=> 8x3 + 12x2 + 6x + 1 - [ ( 2x )3 - 13 ] - 6x + 3 = 15
<=> 8x3 + 12x2 + 4 - 8x3 + 1 = 15
<=> 12x2 + 15 = 15
<=> 12x2 = 0
<=> x = 0
2) x( x - 4 )( x + 4 ) - ( x - 5 )( x2 + 5x + 25 ) = 13
<=> x( x2 - 16 ) - ( x3 - 53 ) = 13
<=> x3 - 16x - x3 + 125 = 13
<=> 125 - 16x = 13
<=> 16x = 112
<=> x = 7
Bài 2.
A = ( x + 5 )( x2 - 5x + 25 ) - ( 2x + 1 )3 - 28x3 + 3x( -11x + 5 )
= x3 + 53 - ( 8x3 + 12x2 + 6x + 1 ) - 28x3 - 33x2 + 15x
= -27x3 + 125 - 8x3 - 12x2 - 6x - 1 - 33x2 + 15x
= -33x3 - 45x2 + 9x + 124 ( có phụ thuộc vào biến )
B = ( 3x + 2 )3 - 18x( 3x + 2 ) + ( x - 1 )3 - 28x3 + 3x( x - 1 )
= 27x3 + 54x2 + 36x + 8 - 54x2 - 36x + x3 - 3x2 + 3x - 1 - 28x3 + 3x2 - 3x
= 7 ( đpcm )
C = ( 4x - 1 )( 16x2 + 4x + 1 ) - ( 4x + 1 )3 + 12( 4x + 1 )3 + 12( 4x + 1 ) - 15
= ( 4x )3 - 13 - [ ( 4x + 1 )3 - 12( 4x + 1 )3 - 12( 4x + 1 ) ] - 15
= 64x3 - 1 - ( 4x + 1 )[ ( 4x + 1 )2 - 12( 4x + 1 )2 - 12 ] - 15
= 64x3 - 16 - ( 4x + 1 )[ 16x2 + 8x + 1 - 12( 16x2 + 8x + 1 ) - 12 ]
= 64x3 - 16 - ( 4x + 1 )( 16x2 + 8x - 11 - 192x2 - 96x - 12 )
= 64x3 - 16 - ( 4x + 1 )( -176x2 - 88x - 23 )
= 64x3 - 16 - ( -704x3 - 528x2 - 180x - 23 )
= 64x3 - 16 + 704x3 + 528x2 + 180x + 23
= 768x3 + 528x2 + 180x + 7 ( có phụ thuộc vào biến )

\(a,5\left(x^2-3x+1\right)+x\left(1-5x\right)=x-2\)
\(\Leftrightarrow5x^2-15x+5+x-5x^2-x+2=0\)
\(\Leftrightarrow-15x+7=0\)
\(\Leftrightarrow-15x=-7\)
\(\Leftrightarrow x=-\frac{7}{-15}\)
\(\Leftrightarrow x=\frac{7}{15}\)

a) \(3\left(x^2-2x+1\right)+x\left(2-3x\right)=7\)
\(\Rightarrow3x^2-6x+3+2x-3x^2=7\)
\(\Rightarrow-4x+3=7\)
\(\Rightarrow-4x+3-7=0\)
\(\Rightarrow-4x-4=0\)
\(\Rightarrow-4\left(x+1\right)=0\)
\(\Rightarrow x+1=0\)
\(\Rightarrow x=-1\)
b) \(5\left(x-2\right)+2\left(x+3\right)=10\)
\(\Rightarrow5x-10+2x+6=10\)
\(\Rightarrow7x-4=10\)
\(\Rightarrow7x=10+4=14\)
\(\Rightarrow x=\dfrac{14}{7}=2\)
c) \(\left(x+1\right)\left(-3\right)+5\left(x-4\right)=-3\)
\(\Rightarrow-3x-3+5x-20=-3\)
\(\Rightarrow2x-23=-3\)
\(\Rightarrow2x=-3+23=20\)
\(\Rightarrow x=\dfrac{20}{2}=10\)
d) \(2\left(x-1\right)-x\left(3-x\right)=x^2\)
\(\Rightarrow2x-2-3x+x^2=x^2\)
\(\Rightarrow-x-2+x^2-x^2=0\)
\(\Rightarrow-x-2=0\)
\(\Rightarrow-x=2\)
\(\Rightarrow x=-2\)
đ) \(3x\left(x+5\right)-2\left(x+5\right)=3x^2\)
\(\Rightarrow3x^2+15x-2x-10=3x^2\)
\(\Rightarrow3x^2-3x^2+13x-10=0\)
\(\Rightarrow13x-10=0\)
\(\Rightarrow13x=10\)
\(\Rightarrow x=\dfrac{10}{13}\)
e) \(4x\left(x+2\right)+x\left(4-x\right)=3x^2+12\)
\(\Rightarrow4x^2+8x+4x-x^2=3x^2+12\)
\(\Rightarrow3x^2+12x=3x^2+12\)
\(\Rightarrow3x^2+12x-3x^2-12=0\)
\(\Rightarrow12\left(x-1\right)=0\)
\(\Rightarrow x-1=0\)
\(\Rightarrow x=1\)
f) \(\dfrac{1}{3}x\left(3x+6\right)-x\left(x-5\right)=9\)
\(\Rightarrow x^2+2x-x^2+5x=9\)
\(\Rightarrow7x=9\)
\(\Rightarrow x=\dfrac{9}{7}\)

a)(x+2).(x+3)-(x-2).(x+5)=10
( x^2 +3x+2x+6)-(x^2 +5x-2x-10)=10
x^2 +3x+2x+6-x^2 -5x+2x+10-10=0
2x+6=0
2x=-6
x=-3

a) 4 ( x + 5 )( x + 6 )( x + 10 )( x + 12 ) = 3x2
Do x = 0 không là nghiệm pt nên chia 2 vế pt cho \(x^2\ne0\), ta được :
\(\frac{4}{x^2}\left(x^2+60+17x\right)\left(x^2+60+16x\right)=3\)
\(\Leftrightarrow4\left(x+\frac{60}{x}+17\right)\left(x+\frac{60}{x}+16\right)=3\)
Đến đây ta đặt \(x+\frac{60}{x}+16=t\left(1\right)\)
Ta được :
\(4t\left(t+1\right)=3\Leftrightarrow4t^2+4t-3=0\Leftrightarrow\left(2t+3\right)\left(2t-1\right)=0\)
Từ đó ta lắp vào ( 1 ) tính được x