
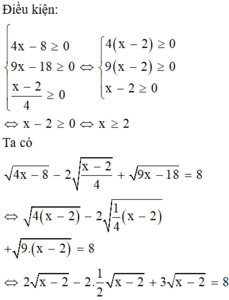
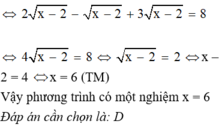
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


c, \(\sqrt{9x-9}-2\sqrt{x-1}=8\left(đk:x\ge1\right)\)
\(< =>\sqrt{9\left(x-1\right)}-2\sqrt{x-1}=8\)
\(< =>\sqrt{9}.\sqrt{x-1}-2\sqrt{x-1}=8\)
\(< =>3\sqrt{x-1}-2\sqrt{x-1}=8\)
\(< =>\sqrt{x-1}=8< =>\sqrt{x-1}=\sqrt{8}^2=\left(-\sqrt{8}\right)^2\)
\(< =>\orbr{\begin{cases}x-1=8\\x-1=-8\end{cases}< =>\orbr{\begin{cases}x=9\left(tm\right)\\x=-7\left(ktm\right)\end{cases}}}\)
d, \(\sqrt{x-1}+\sqrt{9x-9}-\sqrt{4x-4}=4\left(đk:x\ge1\right)\)
\(< =>\sqrt{x-1}+\sqrt{9\left(x-1\right)}-\sqrt{4\left(x-1\right)}=4\)
\(< =>\sqrt{x-1}+\sqrt{9}.\sqrt{x-1}-\sqrt{4}.\sqrt{x-1}=4\)
\(< =>\sqrt{x-1}+3\sqrt{x-1}-2\sqrt{x-1}=4\)
\(< =>\sqrt{x-1}\left(1+3-2\right)=4< =>2\sqrt{x-1}=4\)
\(< =>\sqrt{x-1}=\frac{4}{2}=2=\sqrt{2}^2=\left(-\sqrt{2}\right)^2\)
\(< =>\orbr{\begin{cases}x-1=2\\x-1=-2\end{cases}< =>\orbr{\begin{cases}x=3\left(tm\right)\\x=-1\left(ktm\right)\end{cases}}}\)

Đăng 1 lúc mà nhiều thế. Lần sau đăng 1 câu thôi b.
b/ \(\sqrt{x^2-4x+5}+\sqrt{x^2-4x+8}+\sqrt{x^2-4x+9}=3+\sqrt{5}\)
\(\Leftrightarrow\sqrt{\left(x-2\right)^2+1}+\sqrt{\left(x-2\right)^2+4}+\sqrt{\left(x-2\right)^2+5}=3+\sqrt{5}\)
Ta có: \(VT\ge1+2+\sqrt{5}=3+\sqrt{5}\)
Dấu = xảy ra khi \(x=2\)
c/ \(\sqrt{2-x^2+2x}+\sqrt{-x^2-6x-8}=\sqrt{3-\left(x-1\right)^2}+\sqrt{1-\left(x+3\right)^2}\)
\(\le1+\sqrt{3}\)
Dấu = không xảy ra nên pt vô nghiệm
Câu d làm tương tự
\(a,\sqrt{x^2-4}-x^2+4=0\)
\(\Leftrightarrow\sqrt{x^2-4}=x^2-4\)
\(\Leftrightarrow x^2-4=\left(x-4\right)^2\)
\(\Leftrightarrow x^2-4-x^4+8x^2-16=0\)
\(\Leftrightarrow-x^4-7x^2-20=0\)
\(\Leftrightarrow-\left(x^4+7x^2+\frac{49}{4}\right)-\frac{31}{4}=0\)
\(\Leftrightarrow-\left(x^2+\frac{7}{2}\right)^2=\frac{31}{4}\)
\(\Leftrightarrow\left(x^2+\frac{7}{2}\right)=-\frac{31}{4}\)
\(\Rightarrow\)pt vô nghiệm

Giải câu d thôi mấy câu còn lại đơn giản lắm nên bạn tự làm.
d/ \(\sqrt{x+3-4\sqrt{x-1}}+\sqrt{x+8-6\sqrt{x-1}}=1\)
Điều kiện \(x\ge1\)
\(\Leftrightarrow\sqrt{x-1-4\sqrt{x-1}+4}+\sqrt{x-1-6\sqrt{x-1}+9}=1\)
\(\Leftrightarrow\sqrt{\left(2-\sqrt{x-1}\right)^2}+\sqrt{\left(3-\sqrt{x-1}\right)^2}=1\)
\(\Leftrightarrow|2-\sqrt{x-1}|+|3-\sqrt{x-1}|=1\)
Đây chỉ là phương trình cơ bản của trị tuyệt đối lớp 6, 7 học rồi nên bạn tự làm nhé.

a)\(\sqrt{x^2-9}+\sqrt{x^2-6x+9}=0\)
\(\Rightarrow\sqrt{\left(x-3\right)\left(x+3\right)}+\sqrt{\left(x-3\right)^2}=0\)
\(\Rightarrow\sqrt{\left(x-3\right)\left(x+3\right)}+x-3=0\)
Đặt \(x-3=t\) pt thành
\(\sqrt{t\left(t-6\right)}-t=0\)
\(\Leftrightarrow t^2-6t=t^2\)
\(\Leftrightarrow t=0\)\(\Rightarrow x-3=0\Leftrightarrow x=3\)
b)\(\sqrt{x^2-4}-x^2+4=0\)
\(\Leftrightarrow\sqrt{x^2-4}=x^2-4\)
Đặt \(\sqrt{x^2-4}=t\) pt thành
\(t=t^2\Rightarrow t\left(1-t\right)=0\)
\(\Rightarrow\left[\begin{array}{nghiempt}t=1\\t=0\end{array}\right.\).
Với \(t=0\Rightarrow\sqrt{x^2-4}=0\Rightarrow x=\pm2\)
Với \(t=1\Rightarrow\sqrt{x^2-4}=1\)\(\Rightarrow x=\pm\sqrt{5}\)

Lời giải:
a) ĐK: \(x>0; x\neq 25; x\neq 36\)
PT \(\Rightarrow (\sqrt{x}-2)(\sqrt{x}-6)=(\sqrt{x}-5)(\sqrt{x}-4)\)
\(\Leftrightarrow x-8\sqrt{x}+12=x-9\sqrt{x}+20\)
\(\Leftrightarrow \sqrt{x}=8\Rightarrow x=64\) (thỏa mãn)
Vậy.......
b)
ĐK: \(x\geq \frac{-1}{2}\)
PT \(\Leftrightarrow \sqrt{9(2x+1)}-\sqrt{4(2x+1)}+\frac{1}{3}\sqrt{2x+1}=4\)
\(\Leftrightarrow 3\sqrt{2x+1}-2\sqrt{2x+1}+\frac{1}{3}\sqrt{2x+1}=4\)
\(\Leftrightarrow \frac{4}{3}\sqrt{2x+1}=4\Leftrightarrow \sqrt{2x+1}=3\)
\(\Rightarrow x=\frac{3^2-1}{2}=4\) (thỏa mãn)
c)
ĐK: \(x\geq 2\)
PT \(\Leftrightarrow \sqrt{4(x-2)}-\frac{1}{2}\sqrt{x-2}+\sqrt{9(x-2)}=9\)
\(\Leftrightarrow 2\sqrt{x-2}-\frac{1}{2}\sqrt{x-2}+3\sqrt{x-2}=9\)
\(\Leftrightarrow \frac{9}{2}\sqrt{x-2}=9\Leftrightarrow \sqrt{x-2}=2\Rightarrow x=2^2+2=6\) (thỏa mãn)

\(\sqrt{25x^2-10x+1}=4x+9\)
\(\Leftrightarrow\sqrt{\left(5x-1\right)^2}=4x+9\)
\(\Leftrightarrow\left|5x-1\right|=4x+9\)
\(\Leftrightarrow\orbr{\begin{cases}5x-1=4x+9\\5x-1=-4x-9\end{cases}\Leftrightarrow\orbr{\begin{cases}x=10\\x=-\frac{8}{9}\end{cases}}}\)
Vậy ...
\(\sqrt{x^2+2x+1}=\sqrt{x+1}\)
\(\Leftrightarrow\sqrt{\left(x+1\right)^2}=\sqrt{x+1}\)
\(\Leftrightarrow\sqrt{\left(x+1\right)^2}-\sqrt{x+1}=0\)
\(\Leftrightarrow\sqrt{x+1}.\left(\sqrt{x+1}-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}\sqrt{x+1}=0\\\sqrt{x+1}-1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-1\\x=0\end{cases}}}\)
Vậy ...

a, \(\left(\sqrt{x-1}-2\right)^2+\)\(\left(\sqrt{x-1}-3\right)^2\)
xog xét 2 TH
b, bình phương
2
GTLN : 2 dấu = xra \(2\le x\le4\)

a/ ĐK: \(x \ge -1\). Đặt \(\sqrt{x+1}=a \ge 0\)
PT: \(\Leftrightarrow6a-3a-2a=5\)
\(\Leftrightarrow a=5\)
\(\Leftrightarrow x+1=15\Leftrightarrow x=24\) (nhận)
b,c: Hai ý này đều làm theo cách bình phương hoặc đưa về phương trình chứa dấu giá trị tuyệt đối được nhé.
b) Cách 1: ĐKXĐ: Tự tìm
\(\sqrt{x^{2}-4x+4}=2\Leftrightarrow x^{2}-4x+4=4\Leftrightarrow x(x-4)=0\)
\(\Leftrightarrow x=0\) hoặc \(x=4\) cả 2 cái này đều TMĐK
Cách 2: \((\sqrt{x^2-4x+4}=2)\)
\(\Leftrightarrow \sqrt{(x-2)^2}=2\)
\(\Leftrightarrow \mid x-2\mid=2\)
Với \(x\geq 2\) thì :
\(x-2=2 \Leftrightarrow x=4\) (nhận)
Với \(x<2\) thì
\(-x-2=2\Leftrightarrow x=0\) (nhận)
Vậy \(S={0;4}\)
c) Cách 1: \(\sqrt{x^{2}-6x+9}=x-2\Leftrightarrow \left\{\begin{matrix}x\geq 2 \\ x^{2}-6x+9=x^{2}-4x+4 \end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix}x\geq 2 \\ x=\frac{5}{2} \end{matrix}\right.\)
Nghiệm TMĐK
Cách 2: \((\sqrt{x^2-6x+9}=x-2)\)
\(\Leftrightarrow \mid x-3\mid =x-2\)
Với \(x\geq 3\) thì
\(x-3=x-2\Leftrightarrow 0x=-1\) ( vô lý)
Với \(x<3\) thì
\(-x+3=x-2\Leftrightarrow -2x=-5 \Leftrightarrow x=\frac{5}{2}\)
Vậy \(S={\frac{5}{2}}\)
d) ĐKXĐ: Tự tìm
\(\sqrt{x^{2}+4}=\sqrt{2x+3}\Leftrightarrow x^{2}+4=2x+3\Leftrightarrow x^{2}-2x+1=0\Leftrightarrow (x-1)^{2}=0\)
\(\Leftrightarrow x=1\)
e) ĐKXĐ: \(x\geq \frac{3}{2}\)
\(\frac{\sqrt{2x-3}}{\sqrt{x-1}}=2\Leftrightarrow \frac{2x-3}{x-1}=4\Rightarrow 2x-3=4x-4\Leftrightarrow x=\frac{1}{2}\)
Nghiệm không TMĐK.
Phương trình vô nghiệm.
f) ĐKXĐ: \(x\geq \frac{-15}{2}\)
\(x+\sqrt{2x+15}=0\Leftrightarrow 2x+2\sqrt{2x+15}=0\Leftrightarrow 2x+15+2\sqrt{2x+15}+1-16=0\)
\(\Leftrightarrow (\sqrt{2x+15}+1)^{2}-4^{2}=0\Leftrightarrow (\sqrt{2x+15}+5)(\sqrt{2x+15}-3)=0\)
\(\Leftrightarrow \sqrt{2x+15}-3=0\Leftrightarrow \sqrt{2x+15}=3\Leftrightarrow 2x+15=9\Leftrightarrow x=-3\) (TMĐK)

a) \(\sqrt{4+2x-x^2}=x-2\)
\(\Leftrightarrow\left(\sqrt{4+2x-x^2}\right)^2=\left(x-2\right)^2\)
\(\Leftrightarrow4+2x-x^2=x^2-4x+4\)
\(\Leftrightarrow-x^2+6x=0\)
\(\Leftrightarrow x\left(6-x\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x=0\\6-x=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=0\\x=6\end{cases}}\)
hình như bài này sai đó! em mới học lớp 8 thôi !
lê thị thu huyền:
sai rồi đó em, nhưng mà nhờ em chị mới biết chị sai chỗ nào. Không hiểu đầu óc kiểu gì mà lại thấy 2x+4x=8x mới chết chứ !!!