Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) TXĐ: D = [0; + \(\infty\))
\(y'=1+\frac{1}{2\sqrt{x}}\) > 0 với mọi x thuộc D
BBT: x y' y 0 +oo + 0 +oo
Từ BBT => Hàm số đồng biến trên D ;
y đạt cực tiểu bằng 0 tại x = 0
Hàm số không có cực đại
b) TXĐ : D = = [0; + \(\infty\))
\(y'=1-\frac{1}{2\sqrt{x}}\)
\(y'=0\) <=> \(2\sqrt{x}=1\) <=> \(x=\frac{1}{4}\)
x y' y 0 +oo + 0 +oo -1/4 1/4 0 -
Từ BBT: Hàm số đồng biến trên (1/4; + \(\infty\)); nghịch biến trên (0;1/4)
Hàm số đạt cực tiểu = -1/4 tại x = 1/4
Hàm số không có cực đại

Ta có 64 = -8a + 4b - 2c + d; -61 = 27a + 9b + 3c +d
Từ y ' = 3 a x 2 + 2 b x + c ta thu được hai phương trình 0 = 12a - 4b + c; 0 = 27a + 6b + c
Giải hệ gồm 4 phương trình trên ta thu được a = 2; b = -3; c = -36; d = 20 hay a + b + c + d = -17
Đáp án C

Gỉai
a) Theo đề bài, ta có :
x + y + 12
Vậy, số tự nhiên y là :
( 72 - 12 ) = 30
Và số tự nhiên x là
x - y = 12
30 + 12 = 42
=> Phân số \(\frac{x}{y}\) = \(\frac{7}{5}\)
b) Có 2 cách giải là :
- Cách 1 :
Gọi số cần tiền là n. Theo đề bài, ta có :
\(\frac{x}{y}\) = \(\frac{42-7}{30-n}\) = \(\frac{7}{5}\) => 35 . 5 = 210 - 7n
=> 175 = 210 - 7n
=> n = ( 210 - 175 ) : 7
=> n = 5
- Cách 2 :
\(\frac{x}{y}\) =\(\frac{42-7}{30-n}\) = \(\frac{7}{5}\) => \(\frac{35}{30-n}\) = \(\frac{7}{5}\)
=> 30 - n = 25
=> n = 30 - 25
=> n = 5

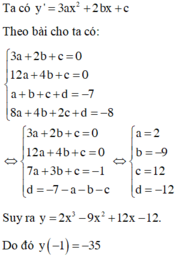



Đáp án C
Ta có
y ' = − 4 x 3 − 16 x = − 4 x x 2 + 4 ; y ' = 0 ⇔ x = 4
Hàm số có một cực trị duy nhất là cực đại tại x = 0 ; y C D = 7