Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

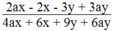 xác định khi 4ax + 6x + 9y + 6ay
≠
0
xác định khi 4ax + 6x + 9y + 6ay
≠
0
⇒ 2x(2a + 3) + 3y(2a + 3) = (2a + 3)(2x + 3y) ≠ 0
Ta có: 2a + 3 ≠ 0 ⇒ a ≠ - 3/2 ; 2x + 3y ≠ 0 ⇒ x ≠ - 3/2 y
Điều kiện: x ≠ - 3/2 y và a ≠ - 3/2
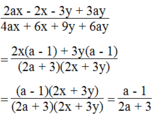
Vậy biểu thức không phụ thuộc vào x, y.

\(\frac{x}{\left(x-y\right)\left(x-z\right)}\) \(+\frac{y}{\left(x-y\right)\left(y-z\right)}\)\(+\frac{z}{\left(y-z\right)\left(z-x\right)}\)
\(=\)\(\frac{x\left(y-z\right)}{\left(x-y\right)\left(x-z\right)\left(y-z\right)}\) \(+\frac{y\left(x-z\right)}{\left(x-y\right)\left(y-z\right)\left(x-z\right)}-\)\(\frac{z\left(x-y\right)}{\left(x-y\right)\left(x-z\right)\left(y-z\right)}\)
\(=\frac{x\left(y-z\right)+y\left(x-z\right)-z\left(x-y\right)}{\left(x-y\right)\left(x-z\right)\left(y-z\right)}\)
\(=\)\(\frac{xy-xz+xy-yz-xz+yz}{\left(x-y\right)\left(x-z\right)\left(y-z\right)}\)
\(=\)\(\frac{2xy-2xz}{\left(x-y\right)\left(x-z\right)\left(y-z\right)}\)
\(=\frac{2x\left(y-z\right)}{\left(x-y\right)\left(x-z\right)\left(y-z\right)}\)
\(=\)\(\frac{2x}{\left(x-y\right)\left(x-z\right)}\)

a/. ĐKXĐ : (x-1)(x+1) # 0 => x # 1 hay x # -1
b/. \(B=\left[\frac{\left(x+1\right)^2}{2\left(x-1\right)\left(x+1\right)}+\frac{3.2}{2\left(x-1\right)\left(x+1\right)}-\frac{\left(x+3\right)\left(x+1\right)}{2\left(x-1\right)\left(x+1\right)}\right].\frac{4\left(x-1\right)\left(x+1\right)}{5}\)
\(B=\frac{x^2+2x+1+6-x^2-4x-3}{2\left(x-1\right)\left(x+1\right)}.\frac{4\left(x-1\right)\left(x+1\right)}{5}\)
\(B=\frac{2\left(4-2x\right)}{5}\)
Em xem lại đè nhé. Đề như vậy thì sẽ ko rút gọn đc hết x trên tử. nên B vẫn phụ thuộc vào biến x.
chao cac bạn và a chi nếu đề sửa lai vây thi minh làm thế nào ( x+1/2x-2 + 3/x^2+1 - x+3/2x+1 )* (4x^2 -1)/5

Bài 1:
a) x≠2x≠2
Bài 2:
a) x≠0;x≠5x≠0;x≠5
b) x2−10x+25x2−5x=(x−5)2x(x−5)=x−5xx2−10x+25x2−5x=(x−5)2x(x−5)=x−5x
c) Để phân thức có giá trị nguyên thì x−5xx−5x phải có giá trị nguyên.
=> x=−5x=−5
Bài 3:
a) (x+12x−2+3x2−1−x+32x+2)⋅(4x2−45)(x+12x−2+3x2−1−x+32x+2)⋅(4x2−45)
=(x+12(x−1)+3(x−1)(x+1)−x+32(x+1))⋅2(2x2−2)5=(x+12(x−1)+3(x−1)(x+1)−x+32(x+1))⋅2(2x2−2)5
=(x+1)2+6−(x−1)(x+3)2(x−1)(x+1)⋅2⋅2(x2−1)5=(x+1)2+6−(x−1)(x+3)2(x−1)(x+1)⋅2⋅2(x2−1)5
=(x+1)2+6−(x2+3x−x−3)(x−1)(x+1)⋅2(x−1)(x+1)5=(x+1)2+6−(x2+3x−x−3)(x−1)(x+1)⋅2(x−1)(x+1)5
=[(x+1)2+6−(x2+2x−3)]⋅25=[(x+1)2+6−(x2+2x−3)]⋅25
=[(x+1)2+6−x2−2x+3]⋅25=[(x+1)2+6−x2−2x+3]⋅25
=[(x+1)2+9−x2−2x]⋅25=[(x+1)2+9−x2−2x]⋅25
=2(x+1)25+185−25x2−45x=2(x+1)25+185−25x2−45x
=2(x2+2x+1)5+185−25x2−45x=2(x2+2x+1)5+185−25x2−45x
=2x2+4x+25+185−25x2−45x=2x2+4x+25+185−25x2−45x
=2x2+4x+2+185−25x2−45x=2x2+4x+2+185−25x2−45x
=2x2+4x+205−25x2−45x=2x2+4x+205−25x2−45x
c) tự làm, đkxđ: x≠1;x≠−1

(x + y)(6x – 6y) ≠ 0 ⇒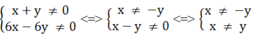
Điều kiện x ≠ ± y
Vậy biểu thức không phụ thuộc vào x, y.