Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

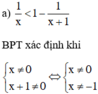
Vậy tập giá trị của x thỏa mãn điều kiện xác định là D = R\{0; –1}

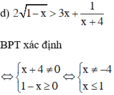
Vậy tập giá trị của x thỏa mãn điều kiện xác định là D = (–∞; 1] \ {–4}.

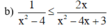
BPT xác định khi
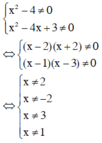
Vậy tập giá trị của x thỏa mãn điều kiện xác định là D = R\{–2; 1; 2; 3}

a) Đkxđ: \(x-5\ne0\Leftrightarrow x\ne5\).
b) Đkxđ: \(x\in R\).
c) Đkxđ: \(x^2-x-2\ge0\)\(\Leftrightarrow\left(x+1\right)\left(x-2\right)\ge0\)
Th1: \(\left\{{}\begin{matrix}x-1\ge0\\x-2\ge0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x\ge1\\x\ge2\end{matrix}\right.\)\(\Leftrightarrow x\ge2\).
Th2: \(\left\{{}\begin{matrix}x-1< 0\\x-2< 0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x< 1\\x< 2\end{matrix}\right.\)\(\Leftrightarrow x< 1\).
Đkxđ: \(\left[{}\begin{matrix}x\ge2\\x< 1\end{matrix}\right.\).
d) Đkxđ: \(x\in R\).

Điều kiện \(x\ge-1\) và \(y\ge-2\). Gọi T là tập giá trị của K. Khi đó \(m\in T\) khi và chỉ khi hệ sau có nghiệm :
\(\begin{cases}x-3\sqrt{x+1}=3\sqrt{y+2}-y\\x+y=m\end{cases}\) \(\Leftrightarrow\begin{cases}3\left(\sqrt{x+1}+\sqrt{y+2}\right)=m\\x+y=m\end{cases}\) (1)
Đặt \(u=\sqrt{x+1};v=\sqrt{y+2}\), điều kiện \(u\ge0;v\ge0\)
Thay vào (1), ta được :
\(\begin{cases}3\left(u+v\right)=m\\u^2+v^2=m+3\end{cases}\) \(\Leftrightarrow\begin{cases}u+v=\frac{m}{3}\\uv=\frac{1}{2}\left(\frac{m^2}{9}-m-3\right)\end{cases}\)
Hay u và v là nghiệm của phương trình :
\(t^2-\frac{m}{3}t+\frac{1}{2}\left(\frac{m^2}{9}-m-3\right)=0\)
\(\Leftrightarrow18t^2-6mt+m^2-9m-27=0\) (2)
Hệ (1) có nghiệm x, y thỏa mãn điều kiện \(x\ge-1\) và \(y\ge-2\) khi và chỉ khi (2) có nghiệm không âm, hay :
\(\begin{cases}\Delta'=-9\left(m^2-18m-54\right)\ge0\\S=\frac{m}{3}\ge0\\P=\frac{m^2-9m-27}{18}\ge0\end{cases}\)
\(\Leftrightarrow\frac{9+3\sqrt{21}}{2}\le m\le9+3\sqrt{15}\)
Vậy \(T=\left[\frac{9+3\sqrt{21}}{2};9+3\sqrt{15}\right]\)
Suy ra Max K = \(\frac{9+3\sqrt{21}}{2}\)
Min K = \(9+3\sqrt{15}\)

\(\Delta'=\left(m-1\right)^2+m^3-\left(m+1\right)^2=m^3-4m\ge0\) \(\Rightarrow\left[{}\begin{matrix}m\ge2\\-2\le m\le0\end{matrix}\right.\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1x_2=-m^3+\left(m+1\right)^2\end{matrix}\right.\)
Do \(x_1+x_2\le4\Rightarrow m-1\le2\Rightarrow m\le3\)
\(\Rightarrow\left[{}\begin{matrix}2\le m\le3\\-2\le m\le0\end{matrix}\right.\)
\(P=x_1^3+x_2^3+3x_1x_2\left(x_1+x_2\right)+8x_1x_2\)
\(=\left(x_1+x_2\right)^3+8x_1x_2\)
\(=8\left(m-1\right)^3+8\left[-m^3+\left(m+1\right)^2\right]\)
\(=8\left(5m-2m^2\right)\)
\(P=8\left(5m-2m^2-2+2\right)=16-8\left(m-2\right)\left(2m-1\right)\le16\)
\(P_{max}=16\) khi \(m=2\)
\(P=8\left(5m-2m^2+18-18\right)=8\left(9-2m\right)\left(m+2\right)-144\ge-144\)
\(P_{min}=-144\) khi \(m=-2\)
BPT xác định khi x + 1 ≠ 0 ⇔ x ≠ –1.
Vậy tập giá trị của x thỏa mãn điều kiện xác định là D = R\{–1}