Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Từ giả thiếtta có thể đặt : \(n^2-1=3m\left(m+1\right)\)với m là 1 số nguyên dương
Biến đổi phương trình ta có :
\(\left(2n-1;2n+1\right)=1\)nên dẫn đến :
TH1 : \(2n-1=3u^2;2n+1=v^2\)
TH2 : \(2n-1=u^2;2n+1=3v^2\)
TH1 :
\(\Rightarrow v^2-3u^2=2\)
\(\Rightarrow v^2\equiv2\left(mod3\right)\)( vô lí )
Còn lại TH2 cho ta \(2n-1\)là số chính phương
b) Ta có :
\(\frac{n^2-1}{3}=k\left(k+1\right)\left(k\in N\right)\)
\(\Leftrightarrow n^2=3k^2+3k+1\)
\(\Leftrightarrow4n^2-1=12k^2+12k+3\)
\(\Leftrightarrow\left(2n-1\right)\left(2n+1\right)=3\left(2k+1\right)^2\)
- Xét 2 trường hợp :
TH1 : \(\hept{\begin{cases}2n-1=3p^2\\2n+1=q^2\end{cases}}\)
TH2 : \(\hept{\begin{cases}2n-1=p^2\\2n+1=3q^2\end{cases}}\)
+) TH1 :
Hệ \(PT\Leftrightarrow q^2=3p^2+2\equiv2\left(mod3\right)\)( loại, vì số chính phương chia 3 dư 0 hoặc 1 )
+) TH2 :
Hệ \(PT\Leftrightarrow p=2a+1\Rightarrow2n=\left(2a+1\right)^2+1\Rightarrow n^2=a^2+\left(a+1\right)^2\)( đpcm )

Đáp án D
Gọi số bé hơn là a; a ∈ N thì số lớn hơn là a + 1
Vì tích của hai số tự nhiên liên tiếp lớn hơn tổng của chúng là 109 nên ta có phương trình:
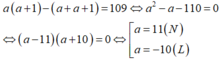
Vậy số bé hơn là 11.

Đáp án D
Gọi số bé hơn là a; a ∈ N* thì số lớn hơn là a + 1 Vì tích của hai số tự nhiên liên tiếp lớn hơn tổng của chúng là 109 nên ta có phương trình:
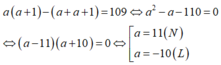
Vậy số bé hơn là 11.

Ta có :
\(\left|a+b\right|< \left|a-b\right|\)
\(\Leftrightarrow\hept{\begin{cases}0< \left|a+b\right|\\0< \left|a-b\right|\end{cases}}\Leftrightarrow\hept{\begin{cases}0< a+b\\0< a-b\end{cases}}\Leftrightarrow\hept{\begin{cases}-a< b\\b< a\end{cases}}\Rightarrow\hept{\begin{cases}a>b\\b< a\end{cases}}\Rightarrow a>b\)

Gọi hai số tự nhiên liên tiếp cần tìm là x và x + 1 ( x ∈ N )
Tích của hai số là: x(x + 1) = x2 + x
Tổng hai số là : x + x + 1 = 2x + 1
Theo bài ra ta có phương trình : \(x^2+x=2x+1+109\)
\(\Leftrightarrow x^2-x-110=0\)
Có a = 1 ; b = -1 ; c = -110
\(\Rightarrow\Delta=\left(-1\right)^2-4.1.\left(-110\right)=441\)
=> Phương trình trên có 2 nghiệm
\(x_1=\frac{1-\sqrt{441}}{2.1}=-10\); \(x_2=\frac{1+\sqrt{441}}{2.1}=11\)
Trong hai nghiệm chỉ có nghiệm x = 11 thỏa mãn điều kiện.
Vậy hai số tự nhiên cần tìm là 11 và 12

Gọi hai số cần tìm là a và a + 1 ( a > 0)
Theo bài ra ta có :
a(a+1) - ( a + a + 1 ) = 109
a^2 + a - 2a - 1 = 109
=> a^2 -a - 1 - 109 = 0
=> a^2 - a - 110 = 0
=> a^2 - 11a + 10a - 110 = 0
=> a(a-11) + 10 ( a - 11 ) = 0
=> ( a + 10 )(a - 11 ) = 0
=> a +1 0 = 0 hoặc a - 11 = 0
=> a = -10 ( loại ) hoặc a = 11
Vậy hai số cần tìm là 11 ; 12

Bài 45. Tích của hai số tự nhiên liên tiếp lớn hơn tổng của chúng là 109. Tìm hai số đó.
Bài giải:
Gọi số bé là x ( x ∈ N, x > 0)
Số lớn là x + 1.( x ∈ N, x > 0)
Tích của số lớn và số bé là x(x -1)
Do tích của hai số lớn và bé lớn hơn tổng của chúng là 109 nên ta có phương tình sau
x(x-1) -(x + x +1) =109
\(\Leftrightarrow\)\(x^2\)-x -2x -1 = 109
\(\Leftrightarrow\)\(x^2\)-x-110 =0
Ta có ∆ = (\(-1^2\))-4.1.(-110)= 441>0 => \(\sqrt{\Delta}\)=\(\sqrt{441}\)=21
Do \(\Delta\)>0 nên phương trình trên có hai nghiệm phân biệt
x1 = \(\dfrac{-1+21}{2.1}\)=11 (thỏa mãn điều kiện của ẩn)
x2 = \(\dfrac{1-21}{2.1}\)=10 (không thỏa mãn điều kiện của ẩn)
\(\Rightarrow\)Số bé là 11
Vậy số lớn là 11+1=12
Đáp số : Số bé:11
Số lớn:12
Gọi số bé là x, x ∈ N, x > 0,
số tự nhiên kề sau là x + 1.
Tích của hai số này là x(x + 1) hay x2 + x.
Theo đầu bài ta có phương trình:
x2 + x - 2x - 1 = 109 hay x2 - x - 110 = 0
Giải phương trình: ∆ = 1 + 440 = 441, √∆ = 21
x1 = 11, x2 = -10
Vì x > 0 nên x2 = -10 không thỏa mãn điều kiện của ẩn.
Vậy hai số cần tìm là 11 và 12

Gọi số bé là x, x ∈ N, x > 0,
số tự nhiên kề sau là x + 1.
Tích của hai số này là x(x + 1) hay x2 + x.
Theo đầu bài ta có phương trình:
x2 + x - 2x - 1 = 109 hay x2 - x - 110 = 0
Giải phương trình: ∆ = 1 + 440 = 441, √∆ = 21
x1 = 11, x2 = -10
Vì x > 0 nên x2 = -10 không thỏa mãn điều kiện của ẩn.
Trả lời: Hai số phải tìm là: 11 và 12
Gọi số bé là x, x ∈ N, x > 0,
số tự nhiên kề sau là x + 1.
Tích của hai số này là x(x + 1) hay x2 + x.
Theo đầu bài ta có phương trình:
x2 + x - 2x - 1 = 109 hay x2 - x - 110 = 0
Giải phương trình: ∆ = 1 + 440 = 441, √∆ = 21
x1 = 11, x2 = -10
Vì x > 0 nên x2 = -10 không thỏa mãn điều kiện của ẩn.
Trả lời: Hai số phải tìm là: 11 và 12
Đáp án D