Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
Bảng phân bố tần số - tần suất
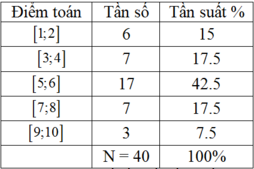
Dựa vào bảng phân bố tần số; tần suất trên ta thấy có 3 lớp có tần suất không bé hơn 17,5% là lớp thứ 2;3 và lớp thứ 4.

a)Số học sinh giỏi lớp 6a là:
40x22,5%=9(học sinh)
Số học sinh trung bình lớp 6a là:
9x200%=18(học sịnh)
Số học sinh khá lớp 6a là:
40-(9+18)=13(học sinh)
b)Tỉ số phần trăm số học sinh trung binh so với cả lớp là:
18:40%=45(%)
Tỉ số phần trăm số học sinh khá so với cả lớp là:
13:40%=32,5(%)

50% = 5/10 ; 2/5 = 4/10
số học sinh nữ là :
45 : (5 + 4) x 5 = 25 (học sinh)
đáp số : 25 học sinh
50%=1/2
Gọi số HS nam là a; số HS nữ là b
Ta có:2/5*a=1/2*b
=>a=1/2*b:2/5
a=1/2:2/5*b
a=5/4*b
Mà a+b=45
Hay 5/4*b+b=45
b*(5/4+1)=45
b*9/4=45
b=45:9/4
b=20(Vô lý vì a=25 mà 25/45=5/9 chứ ko phải là 4/9)
Còn b=25 thì a=20(cũng vô lý vì 50% của 25 thì là 12,5 không thuộc N)
Tui sửa lại đề:2/5 số HS nữ =50% số HS nam
Ta có :1/2*a=2/5*b
=> a=2/5:1/2*b
a=4/5*b
Mà a+b=45
Hay 4/5*b+b=45
b*(4/5+1)=45
b*9/5=45
b=45:9/5
b=25
Vậy số HS nữ của lớp 6a là 25 HS

Gọi số hs của 3 lớp lần lượt là a,b,c
Ta có :
\(a-\frac{1}{4}a=b-\frac{1}{7}b=c-\frac{1}{3}c\) và \(a+b+c=144\)
\(\Leftrightarrow\frac{3a}{4}=\frac{6b}{7}=\frac{2c}{3}\)
\(\Leftrightarrow\frac{a}{\frac{4}{3}}=\frac{b}{\frac{7}{6}}=\frac{c}{\frac{3}{2}}\)
Theo tính chất dãy tỉ số bằng nhau ta có :
\(\frac{a}{\frac{4}{3}}=\frac{b}{\frac{7}{6}}=\frac{c}{\frac{3}{2}}=\frac{a+b+c}{\frac{4}{3}+\frac{7}{6}+\frac{3}{2}}=\frac{144}{4}=36\)
\(\Leftrightarrow\left\{{}\begin{matrix}\frac{a}{\frac{4}{3}}=36\\\frac{b}{\frac{7}{6}}=36\\\frac{c}{\frac{3}{2}}=36\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=48\\b=42\\c=54\end{matrix}\right.\)
Vậy...

Bài 1. Ta có: \(a\left(a+2\right)\left(a-1\right)^2\ge0\therefore\frac{1}{4a^2-2a+1}\ge\frac{1}{a^4+a^2+1}\)
Thiết lập tương tự 2 BĐT còn lại và cộng theo vế rồi dùng Vasc (https://olm.vn/hoi-dap/detail/255345443802.html)
Bài 5: Bất đẳng thức này đúng với mọi a, b, c là các số thực. Chứng minh:
Quy đồng và chú ý các mẫu thức đều không âm, ta cần chứng minh:
\(\frac{1}{2}\left(a^2+b^2+c^2-ab-bc-ca\right)\Sigma\left[\left(a^2+b^2\right)+2c^2\right]\left(a-b\right)^2\ge0\)
Đây là điều hiển nhiên.



Chọn A.
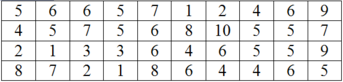
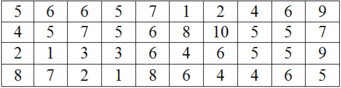
Bảng phân bố tần số - tần suất
Dựa vào bảng trên ta thấy lớp 3 có tần số và tần suất cao nhất; lớp 5 có tần số; tần suất thấp nhất.
Lớp 2 và 4 có cùng tần số và tần suất.