

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Nhiệt lượng cần cung cấp để đun sôi 1,5 lít nước là:
Q = 420000.1,5 = 630000 J
Theo công thức tính nhiệt lượng tỏa ra của ấm ta có:
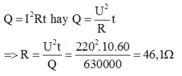
→ Đáp án C

Nhiệt lượng cần thiết để đun sôi 1 lít nước là: Q 0 = m 0 . c . ∆ t 0
Nhiệt lượng cần thiết để đun sôi 1,5 lít nước là:
Q = m . c . ∆ t 0 = 1,5 m 0 .c. △ t 0 = 1,5. Q 0 = 630000 (J) (vì m = 1,5kg = 1,5. m 0 )
Mặt khác: 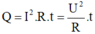
→ Điện trở của dây nung: 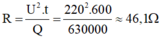

- Tính được điện trở cuả dây xoắn là:
\(R=p\frac{l}{s}=5,4.10^{-4}.\frac{10}{0,2.10^{-6}}=27\left(\Omega\right)\)
- Cường độ dòng điện qua bếp : I = \(I=\frac{U}{R}=\frac{220}{27}=8,14\left(A\right)\)
- Tính được nhiệt lượng cần cho nước đã cho đến sôi(Q hữu ích):
Q = cm(t2 – t1) = 4200 J/kg.K.2kg.(100 -15) = 714000J
- Do bếp có hiệu suất nên nhiệt lượng bếp phải cấp :
\(H=\frac{Qi}{Q}.100\%\)80% =>\(Q=\frac{Qi.100\%}{H}=\frac{71400.100\%}{80\%}=892500\left(J\right)\)
- Nhiệt lượng này do điện năng chuyển thành từ dây xoắn. Vậy thời gian cần thiết cho nước sôi :
Q = A = U.I.t = >t = \(\frac{Q}{UI}=\frac{892500}{220.8,14}=497,8\left(s\right)\) = 8,3(phút)
cái đáp án điện trở có phải sai rồi không ? Tôi bấm máy nó lại ra 27000 ohm ấy

\(A=2,5.420000=1050000\left(J\right)\)
\(A=P.t=\dfrac{U^2}{R}.t\Rightarrow R=\dfrac{U^2.t}{A}=\dfrac{220^2.18.60}{1050000}\approx50\left(\Omega\right)\)

Nhiệt lượng cần để tăng nhiệt độ của ấm nhôm từ 25oC tới 100oC là:
\(Q_1=m_1.c_1\left(t_2-t_1\right)=0,5.880.100-25=33000\left(J\right)\)
Nhiệt lượng cần để tăng nhiệt độ của nước từ 25oC tới 100oC là:
\(Q_2=m.c\left(t_2-t_1\right)=2.4200.\left(100-25\right)=630000\left(J\right)\)
Nhiệt lượng tổng cộng cần thiết:
\(Q=Q_1+Q_2=33000+630000=663000\left(J\right)\) (1)
Mặt khác nhiệt lượng có ích để đun nước do ấm điện cung cấp trong thời gian 20 phút là:
\(H=\frac{Q}{Q_{tp}}\Rightarrow Q=H.Q_{tp}\)
Ta lại có: \(Q_{tp}=A=P.t\)
\(\Rightarrow Q=H.P.t\Rightarrow P=\frac{Q}{H.t}\) (2)
Tính hiệu suất:
\(\text{H = 100% - 30% = 70%}\)
Từ (1) và (2) \(\Rightarrow P=\frac{Q}{H.t}=\frac{663000.100}{70.1200}=789,3\left(W\right)\)

* Gọi Q (J) là nhiệt lượng mà bếp cần cung cấp cho ấm để đun sôi nước thì Q luôn không đổi trong các trường hợp trên. Nếu ta gọi t1 ; t2 ; t3 và t4 theo thứ tự là thời gian bếp đun sôi nước tương ứng với khi dùng R1, R2 nối tiếp; R1, R2 song song ; chỉ dùng R1 và chỉ dùng R2 thì theo định luật Jun-lenxơ ta có :
\(Q=\frac{U^2.t}{R}=\frac{U^2.t_1}{R_1+R_2}=\frac{U^2.t_2}{\frac{R_1.R_2}{R_1+R_2}}=\frac{U^2.t_3}{R_1}=\frac{U^2.t_4}{R_2}\) (1)
* Ta tính R1 và R2 theo Q; U ; t1 và t2 :
+ Từ (1) \(\Rightarrow\) R1 + R2 = \(R_1+R_2=\frac{U^2t_1}{Q}\)
+ Cũng từ (1) \(\Rightarrow\) R1 . R2 = \(R_1.R_2=\frac{U^2t_2}{Q}\left(R_1+R_2\right)=\frac{U^4t_1t_2}{Q^2}\)
* Theo định lí Vi-et thì R1 và R2 phải là nghiệm số của phương trình :
R2 - \(\frac{U^2t_1}{Q}.R+\frac{U^4t_1t_2}{Q^2}=0\)(1)
Thay t1 = 50 phút ; t2 = 12 phút vào PT (1) và giải ta có \(\Delta=10^2.\frac{U^2}{Q^2}\Rightarrow\sqrt{\Delta}=\frac{10.U^2}{Q}\) .
\(\Rightarrow\) \(R_1=\frac{\frac{U^2t_1}{Q}+\frac{10U^2}{Q}}{2}=\frac{\left(t_1+t_2\right)U^2}{2Q}=30\frac{U^2}{Q}\) và \(R_2=20.\frac{U^2}{Q}\)
* Ta có \(t_3=\frac{Q.R_1}{U^2}\)= 30 phút và \(t_4=\frac{Q.R_2}{U^2}\) = 20 phút . Vậy nếu dùng riêng từng điện trở thì thời gian đun sôi nước trong ấm tương ứng là 30 phút và 20 phút .