Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
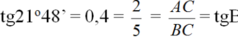
Suy ra y = 21o48'
=> x = 90o - y = 68o12' (x, y là hai góc phụ nhau)
Vậy x – y = 68o12' - 21o48' = 46o24'


Ta có tgy =2/5 = 0,4 ⇒ tgy= tg21048′ ⇒ y= 21048′
x = 900 – 21048′ = 68012′
x – y = 68012′ -21048′ = 46024′
tgy=25=0,4tgy=25=0,4 nên y ≈ 21°48’
Do đó: x = 90° - y ≈ 68°12’
Vậy: x – y ≈ 68°12’ - 21°48’ ≈ 46°24’
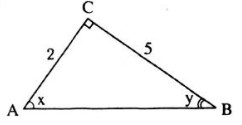

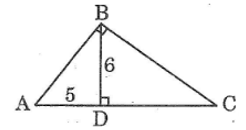
a) Vì tam giác ABD vuông tại D nên ta có:
SΔABD=12.BD.AD=12.6.5=15(đvdt)
b) Ta có: tgˆC=BD/DCt
Theo giả thiết: tgˆC=3/4
Suy ra: BD/DC=3/4⇒DC=4/3 BD=4.6/3=8 A B C 6 5
Suy ra: AC=AD+DC=5+8=13.

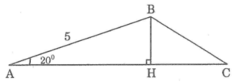
Kẻ BH vuông góc với AC
Xét ΔABH vuông tại H có \(BH=AB\cdot\sin A\simeq1,7101\left(cm\right)\)
\(S_{ABC}=\dfrac{BH\cdot AC}{2}=6.8404\left(cm^2\right)\)

1) a) Từ C dựng đường cao CF
Ta có: \(\sin A=\frac{CF}{b};\sin B=\frac{CF}{a}\)\(\Rightarrow\)\(\frac{\sin A}{\sin B}=\frac{\frac{CF}{b}}{\frac{CF}{a}}=\frac{a}{b}\)\(\Leftrightarrow\)\(\frac{a}{\sin A}=\frac{b}{\sin B}\) (1)
Từ A dựng đường cao AH
Có: \(\sin B=\frac{AH}{c};\sin C=\frac{AH}{b}\)\(\Rightarrow\)\(\frac{\sin B}{\sin C}=\frac{\frac{AH}{c}}{\frac{AH}{b}}=\frac{b}{c}\)\(\Leftrightarrow\)\(\frac{b}{\sin B}=\frac{c}{\sin C}\) (2)
(1), (2) => đpcm
b) từ a) ta có: \(\hept{\begin{cases}\sin A=\frac{CF}{b}\\\cos A=\frac{AF}{b}\end{cases}\Leftrightarrow\hept{\begin{cases}CF=b.\sin A\\AF=b.\cos A\end{cases}}}\)
Có: \(BF=c-AF=c-b.\cos A\)
Py-ta-go:
\(a^2=BF^2+CF^2=\left(c-b.\cos A\right)^2+\left(b.\sin A\right)^2=c^2+b^2.\cos^2A+b^2.\sin^2A-2bc.\cos A\)
\(=b^2\left(\sin^2A+\cos^2A\right)+c^2-2bc.\cos A=b^2+c^2-2bc.\cos A\) (đpcm)
c) Có: \(\hept{\begin{cases}\cos A=\frac{AF}{b}\\\cos B=\frac{BF}{a}\end{cases}\Rightarrow b.\cos A+a.\cos B=b.\frac{AF}{b}+a.\frac{BF}{a}=AF+BF=c}\)
bài 2 mk có làm r bn ib mk gửi link nhé
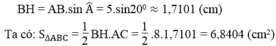
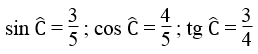

Ta có:
Suy ra y = 21 ° 48 '
= > x = 90 ° - y = 68 ° 12 ' (x, y là hai góc phụ nhau)
Vậy x – y = 68 ° 12 ' - 21 ° 48 ' = 46 ° 24 '