Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: BC2 = AC2 + AB2 – 2AB.AC. cos1200
=> BC2 = m2 + n2 – 2m.n ()
=> BC2 = m2 + n2 + m.n
=> BC =
Ta có
a2 = 82 + 52 – 2.8.5 cos 1200 = 64 + 25 + 40 = 129
=> a = √129 ≈ 11, 36cm
Ta có thể tính góc B theo định lí cosin
cosB = =
≈ 0,7936 =>
= 37048’
Ta cũng có thể tính góc B theo định lí sin :
cosB = =
=> sinB ≈ 0,6085 =>
= 37048’
Tính C từ = 1800– (
+
) =>
≈ 22012’

Từ định lí cosin a2 = b2 + c2 – 2bc. cosA
ta suy ra cos A = =
=> cosA ≈ 0,8089 => = 360
Tương tự, ta tính được ≈ 1060 28’ ;
≈ 370 32’.

Ta có: = 1800 – (
+
) = 400
Áp dụng định lí sin :
=
=
, ta có:
b = ≈ 212,32cm
c = ≈ 179,40cm

= 320; b = a.cos320 => b ≈ 61,06cm; c = a.sin320 ≈ 38,15cm
ha = => ha ≈ 32,35cm


Ta có +
=
=
= a
Ta có: –
=
+
.
Trên tia CB, ta dựng =
=> –
=
+
=
Tam giác EAC vuông tại A và có : AC = a, CE = 2a , suy ra AE = a√3
Vậy =
= a√3

Trước hết ta có
= 3
=>
= 3 (
+
)
=> = 3
+ 3
=> – = 3
=> =
mà =
–
nên
=
(
–
)
Theo quy tắc 3 điểm, ta có
=
+
=>
=
+
–
=> = –
+
hay
= –
+

a) Gọi theo thứ tự ∆1, ∆2, ∆3 là giá của các vectơ ,
,
cùng phương với
=> ∆1 //∆3 ( hoặc ∆1 = ∆3 ) (1)
cùng phương với
=> ∆2 // ∆3 ( hoặc ∆2 = ∆3 ) (2)
Từ (1), (2) suy ra ∆1 // ∆2 ( hoặc ∆1 = ∆2 ), theo định nghĩa hai vectơ ,
cùng phương.
Vậy
a) đúng.
b) Đúng.

Ta xét tổng:
+
+
+
+
+
=
=
(1)
Mặt khác, ta có ABIJ, BCPQ và CARS là các hình bình hành nên:
=
=
=
=> +
+
=
+
+
=
=
(2)
Từ (1) và (2) suy ra : +
+
=
(dpcm)


Gọi D là trung điểm của cạnh AB, ta có:
+
= 2
Đẳng thức đã cho trở thành:
2+ 2
=
=> +
=
Đẳng thức này chứng tỏ M là trung điểm của CD
Ta có: BC2 = AC2 + AB2 – 2AB.AC. cos1200
=> BC2 = m2 + n2 – 2m.n (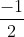 )
)
=> BC2 = m2 + n2 + m.n
=> BC =