Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có các tam giác BAM cân tại B, tam giác CAN cân tại C.
Từ đó \(\widehat{BAM}=\dfrac{180^o-\widehat{B}}{2};\widehat{CAN}=\dfrac{180^o-\widehat{C}}{2}\).
Ta có: \(\widehat{MAN}=\widehat{BAM}+\widehat{CAN}-\widehat{BAC}=\dfrac{180^o-\widehat{B}}{2}+\dfrac{180^o-\widehat{C}}{2}-90^o=\dfrac{360^o-\left(\widehat{B}+\widehat{C}\right)}{2}-90^o=\dfrac{360^o-90^o}{2}-90^o=45^o\)

A B C M N
Ta có
BM=AB suy ra tam giác BAM cân tại B suy ra \(\widehat{BAM}=\frac{180^o-\widehat{B}}{2}\)
CN=AC suy ra tam giác NAC cân tại C suy ra \(\widehat{NAC}=\frac{180^o-\widehat{C}}{2}\)
(nếu cần thì bạn phải cm thêm cả N nằm giữa B và M nhé!)
MÀ ta thấy \(\widehat{BAM}+\widehat{ACN}=\widehat{BAC}+\widehat{NAM}\)
\(\Rightarrow\frac{180^o-\widehat{B}}{2}+\frac{180^o-\widehat{C}}{2}=90^o+\widehat{NAM}\)
\(\Rightarrow\frac{360^o-\left(\widehat{B}+\widehat{C}\right)}{2}=90^o+\widehat{NAM}\)
\(\Rightarrow\frac{360^o-90^o}{2}=90^o+\widehat{NAM}\)
\(\Rightarrow\widehat{NAM}=45^o\)
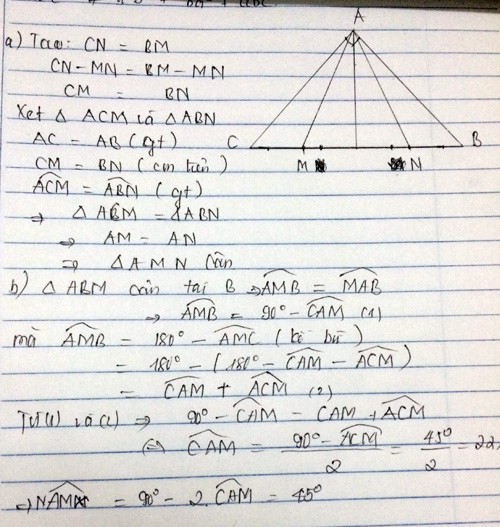
Ta có: BA=BM => tam giác BAM cân tại B
=> \(\widehat{AMB}=\dfrac{180-\widehat{ABC}}{2}\) (tự chứng minh) (1)
Tương tự: tam giác ANC cân tại C
=> \(\widehat{ANC}=\dfrac{180-\widehat{ACB}}{2}\) (2)
Từ 1 và 2 => \(\widehat{AMB}+\widehat{ANC}=\dfrac{180-\widehat{ABC}}{2}+\dfrac{180-\widehat{ACB}}{2}\)
\(\widehat{AMB}+\widehat{ANC}=\dfrac{180-\widehat{ABC}+180-\widehat{ACB}}{2}=\dfrac{360-90}{2}=135\)
=> MAN= 180 -135 = 45 (TỰ CHỨNG MINH)
Vậy MAN = 45
Chúc bạn hk tốt nhớ theo dõi mk vs ạ. Mk xin cảm ơn rất nhiều ạ
cảm ơn bạn nhé