
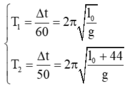

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

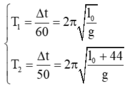


Chọn đáp án A
Δ t = 60.2 π l g = 50.2 π l + 0 , 44 g ⇒ 6 5 = l + 0 , 44 l ⇒ l = 1 m .

Đáp án D
+ Chu kì là thời gian để con lắc thực hiện được một dao động toàn phần
→ T 1 = Δt 60 = 2 π l g T 2 = Δt 50 = l + 44 g → l + 144 l = 60 50 2
→ l = 100 cm.

Đáp án B
Trong cùng một khoảng thời gian t, con lắc thứ nhất thực hiện được 60 dao động toàn phần còn con lắc kia thực hiện được 50 dao động toàn phần. Biết chiều dài dây treo của chúng khác nhau một đoạn 44 cm. Gọi chiều dài của con lắc có dây treo ngắn hơn là l1 và chiều dài của con lắc đơn kia là l2
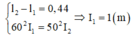

từ công thức \(T=2\pi\sqrt{\frac{l}{g}}\) suy ra \(T^2\) tỷ lệ thuận với \(l\)
Ta có \(\frac{l}{l-16}=\frac{T^2_1}{T^2_2}=\frac{\left(\frac{\Delta t}{6}\right)^2}{\left(\frac{\Delta t}{10}\right)^2}=\frac{25}{9}=\frac{25}{25-16}\)
Vậy l=25cm

Phương pháp:Chu kì dao động là thời gian vật thực hiện hết một dao động toàn phần
Công thức: T = ∆ t N = 2 π l g (N là số dao động toàn phần thực hiện trong thời gian ∆t)
Cách giải:
Ta có:
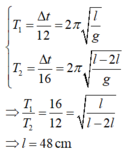
Đáp án C

Chọn B
+ Ta có: Δt = 6T1 = 10T2 → 6 . 2 π l g = 10 . 2 π l - 0 , 16 g
+ Giải phương trình ta được: l = 25cm.