Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

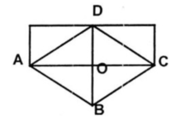
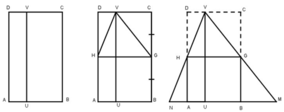
Giả sử ta có hình thoi ABCD, hai đường chéo AC và BD cắt nhau tại O. Ta cắt hình thoi theo đường chéo AC ta được 2 tam giác.
Lấy AC làm một cạnh hình chữ nhật. Cắt tam giác BAC theo đường BO ta được hai tam giác ghép lại ta có hình chữ nhật.

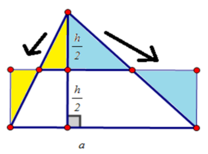
Xét △ ABC. Kẻ đường cao AH. Gọi M là trung điểm của AC, N là trung điểm của AB.
Từ M kẻ đường thẳng song song AH cắt BC tại K
Từ N kẻ đường thẳng song song AH cắt BC tại L
Từ A kẻ đường thẳng song song BC cắt hai đường thẳng MK và NL tại T và R
Ta có: △ MKC = △ MTA
△ NLB = △ NAR
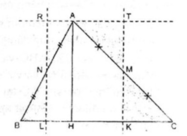
Cắt △ ABC theo đường MK và NL ta ghép lại được một hình chữ nhật KTRL có diện tích bằng diện tích tam giác ABC


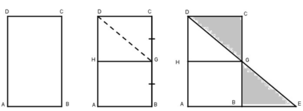
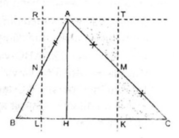



Vì hình thoi có hai đường chéo vuông góc cắt nhau tại trung điểm mỗi đường nên chia hình thoi thành 4 tam giác bằng nhau.
Giả sử hình chữ nhật ABCD ta chọn trung điểm M của CD. Nối AM, BM ta cắt theo đường AM và BM ta ghép lại được một hình thoi.