Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Gọi bán kính đáy khúc gỗ là $r$ (cm) thì:
Thể tích khúc gỗ:
$\pi r^2h=15\pi r^2$ (cm khối)
Thể tích hình nón:
$\frac{1}{3}\pi r^2h=5\pi r^2$ (cm khối)
Thể tích phần bỏ đi:
$15\pi r^2-5\pi r^2=640r$ (cm khối)
$10\pi r^2=640r$
$10\pi r=640$
$r=\frac{64}{\pi}$ (cm)
Thể tích khối nón: $5\pi r^2=5\pi.\frac{64^2}{\pi ^2}=\frac{20480}{\pi}$ (cm khối)
Nghe đề bài có vẻ sai sai. Nếu đề là $640\pi$ (cm khối) thì bạn cũng làm tương tự, $r=8$ (cm)

a) Với giả thiết ở đề bài, ta có thể tính được r từ đó tính được diện tích mặt cầu gần bằng \(26cm^2\)
b) Tương tự câu a, ta tính được thể tích hình nón là \(7,9cm^3\)

Hướng dẫn làm bài:
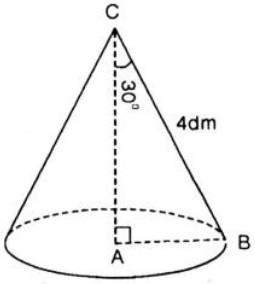
Trong tam giác vuông ABC, ta có:
AB=BC.sinC=BC.sin300=4.1/2=2(dm)
AC=BC.cosC=BC.cos300=4.√3/2=2√3(dm)
Ta có: Sxq = πRl = π. 2. 4 = 8 π (dm2)
V=1/3 π R2 h=1/3 π.22.2√3=8√3.π/3(dm3)

Theo đề bài ta có:
Diện tích hình chữ nhật ABCD là: AB.AD=2a\(^2\) (1)
Chu vi hình chữ nhật là: 2(AB+CD)=6a⇒AB+CD=3a ( 2 )
Từ (1) và (2), ta có ABAB và CDCD là nghiệm của phương trình:
x\(^2\)− 3ax − 2a\(^2\)=0
Giải phương trình ta được: x\(_1\)= 2a; x\(_2\)=a
Theo giả thiết AB>AD nên ta chọn AB=2a; AD=a
Khi quay hình chữ nhật quanh ABAB ta được hình trụ có h=AB=2a và r=AD=a
Vậy diện tích xung quanh hình trụ là:
Sxq=2π.AD.AB=2π.a.2a=4πa\(^2\)
Thể tích hình trụ là:
V=π.AD2.AB=π.a\(^2\).2a=2πa\(^3\)


a, V = 960π c m 3
b, Sxq = 136 c m 2