PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
XO
6 tháng 7 2019
\(\frac{8}{9}-\frac{1}{72}-\frac{1}{56}...-\frac{1}{6}-\frac{1}{2}\)
= \(\frac{8}{9}-\left(\frac{1}{72}+\frac{1}{56}+...+\frac{1}{6}+\frac{1}{2}\right)\)
= \(\frac{8}{9}-\left(\frac{1}{2}+\frac{1}{6}+...+\frac{1}{56}+\frac{1}{72}\right)\)
= \(\frac{8}{9}-\left(\frac{1}{1.2}+\frac{1}{2.3}+...+\frac{1}{7.8}+\frac{1}{8.9}\right)\)
= \(\frac{8}{9}-\left(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{7}-\frac{1}{8}+\frac{1}{8}-\frac{1}{9}\right)\)
= \(\frac{8}{9}-\left(1-\frac{1}{9}\right)\)
= \(\frac{8}{9}-\frac{8}{9}\)
= \(0\)
1 tháng 9 2019
"girl cute" là sai rồi bạn ơi, trong tiếng anh, tính từ (cute) phải đứng trước danh tư (girl).
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
28 tháng 8 2020
\(=\frac{8}{9}+\frac{1}{2}-\left(\frac{1}{3.4}+\frac{1}{4.5}+\frac{1}{5.6}+\frac{1}{6.7}+\frac{1}{7.8}+\frac{1}{8.9}\right)\)
\(=\frac{8}{9}+\frac{1}{2}-\left(\frac{1}{3}-\frac{1}{9}\right)=1+\frac{1}{2}-\frac{1}{3}=1\frac{1}{6}\)
6 tháng 3 2018
A=\(-1\left(\frac{1}{4.5}+\frac{1}{5.6}+\frac{1}{6.7}+\frac{1}{7.8}.+\frac{1}{8.9}+\frac{1}{9.10}\right)\)
=\(-1\left(\frac{1}{4}-\frac{1}{5}+\frac{1}{5}-\frac{1}{6}+\frac{1}{6}-\frac{1}{7}+\frac{1}{7}-\frac{1}{8}+\frac{1}{8}-\frac{1}{9}+\frac{1}{9}-\frac{1}{10}\right)\)
=\(-1\left(\frac{1}{4}-\frac{1}{10}\right)\)=\(-1.\frac{3}{20}=\frac{-3}{20}\)
6 tháng 3 2016
\(A=\frac{1}{6}+\frac{1}{12}+\frac{1}{20}+\frac{1}{30}+\frac{1}{42}+\frac{1}{56}\)
\(A=\frac{1}{2.3}+\frac{1}{3.4}+\frac{1}{4.5}+\frac{1}{5.6}+\frac{1}{6.7}+\frac{1}{7.8}\)
\(A=\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+\frac{1}{5}-\frac{1}{6}+\frac{1}{6}-\frac{1}{7}+\frac{1}{7}-\frac{1}{8}\)
\(A=\frac{1}{2}-\frac{1}{8}\)
\(A=\frac{3}{8}\)
6 tháng 3 2016
\(A=\frac{1}{6}+\frac{1}{12}+\frac{1}{20}+\frac{1}{30}+\frac{1}{42}+\frac{1}{56}\)
\(A=\frac{1}{2.3}+\frac{1}{3.4}+\frac{1}{4.5}+\frac{1}{5.6}+\frac{1}{6.7}+\frac{1}{7.8}\)
\(A=\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+\frac{1}{5}-\frac{1}{6}+\frac{1}{6}-\frac{1}{7}+\frac{1}{7}-\frac{1}{8}\)
\(A=\frac{1}{2}-\frac{1}{8}=\frac{3}{8}\)
mình nhé!
13 tháng 6 2017
A = 1/6 + 1/12 + 1/20 + 1/30 + 1/42 + 1/56
A = (1/6 + 1/12) + 1/20 + 1/30 + 1/42 + 1/56
A = 1/4 + 1/20 + 1/30 + 1/42 + 1/56
A = (1/4 + 1/20) + 1/30 + 1/42 + 1/56
A = 3/10 + 1/30 + 1/42 + 1/56
A = (3/10 + 1/30) + 1/42 + 1/56
A = 1/3 + 1/42 + 1/56
A = (1/3 + 1/42) + 1/56
A = 5/14 + 1/56
A = 3/8
N
1
1 tháng 7 2016
\(B=\frac{1}{6}+\frac{1}{12}+\frac{1}{20}+...+\frac{1}{90}\)
\(B=\frac{1}{2.3}+\frac{1}{3.4}+\frac{1}{4.5}+...+\frac{1}{9.10}\)
\(B=\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+...+\frac{1}{9}-\frac{1}{10}\)
\(B=\frac{1}{2}-\frac{1}{10}\)
\(B=\frac{2}{5}\)
PV
5
HM
3 tháng 8 2016
\(\frac{-1}{90}-\frac{1}{72}-\frac{1}{56}-\frac{1}{42}-\frac{1}{30}-\frac{1}{20}-\frac{1}{12}-\frac{1}{6}-\frac{1}{2}\)
= \(-\left(\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+\frac{1}{20}+\frac{1}{30}+\frac{1}{42}+\frac{1}{56}+\frac{1}{72}+\frac{1}{90}\right)\)
=\(-\left(\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+\frac{1}{4.5}+\frac{1}{5.6}+\frac{1}{6.7}+\frac{1}{7.8}+\frac{1}{8.9}+\frac{1}{9.10}\right)\)
=\(-\left(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+\frac{1}{5}-\frac{1}{6}+\frac{1}{6}-\frac{1}{7}+\frac{1}{7}-\frac{1}{8}+\frac{1}{8}-\frac{1}{9}+\frac{1}{9}-\frac{1}{10}\right)\)
=\(-\left(1-\frac{1}{10}\right)=-\left(\frac{9}{10}\right)=-\frac{9}{10}\)
BB
3 tháng 8 2016
\(\frac{-1}{90}-\frac{-1}{72}-\frac{-1}{56}-\frac{-1}{42}-\frac{-1}{30}-\frac{-1}{20}-\frac{-1}{12}-\frac{-1}{6}-\frac{-1}{2}\)
\(=\frac{-1}{10.9}-\frac{-1}{9.8}-\frac{-1}{8.7}-\frac{-1}{7.6}-\frac{-1}{6.5}-\frac{-1}{5.4}-\frac{-1}{4.3}-\frac{-1}{3.2}-\frac{-1}{2.1}\)
23 tháng 1 2020
\(a,A=\frac{-1}{20}+\frac{-1}{30}+\frac{-1}{42}+\frac{-1}{56}+\frac{-1}{72}+\frac{-1}{90}\)
\(=\frac{-1}{4.5}+\frac{-1}{5.6}+\frac{-1}{6.7}+\frac{-1}{7.8}+\frac{-1}{8.9}+\frac{-1}{9.10}\)
\(=\frac{-1}{4}+\frac{1}{5}-\frac{1}{5}+\frac{1}{6}-...-\frac{1}{9}+\frac{1}{10}\)
\(=-\frac{1}{4}+\frac{1}{10}\)
\(=-\frac{3}{20}\)
\(b,B=\frac{5}{2.1}+\frac{4}{1.11}+\frac{3}{11.2}+\frac{1}{2.15}+\frac{13}{15.4}\)
\(\frac{B}{7}=\frac{5}{2.7}+\frac{4}{11.7}+\frac{3}{11.14}+\frac{1}{14.15}+\frac{13}{15.28}\)
\(=\frac{1}{2}-\frac{1}{7}+\frac{1}{7}-\frac{1}{11}+\frac{1}{11}-....-\frac{1}{28}\)
\(=\frac{1}{2}-\frac{1}{28}=\frac{13}{28}\)
CC
23 tháng 1 2020
a) \(A=\frac{-1}{20}+\frac{-1}{30}+\frac{-1}{42}+\frac{-1}{56}+\frac{-1}{72}+\frac{-1}{90}\)
\(\Rightarrow-1.A=\frac{1}{20}+\frac{1}{30}+........+\frac{1}{90}\)
\(=\frac{1}{4.5}+\frac{1}{5.6}+........+\frac{1}{9.10}\)
\(=\frac{1}{4}-\frac{1}{5}+\frac{1}{5}-\frac{1}{6}+........+\frac{1}{9}-\frac{1}{10}=\frac{1}{4}-\frac{1}{10}=\frac{3}{20}\)
\(\Rightarrow A=\frac{3}{20}:\left(-1\right)=\frac{-3}{20}\)
b) \(B=\frac{5}{2.1}+\frac{4}{1.11}+\frac{3}{11.2}+\frac{1}{2.15}+\frac{13}{15.4}\)
\(\Rightarrow\frac{1}{7}B=\frac{5}{2.7}+\frac{4}{7.11}+\frac{3}{11.14}+\frac{1}{14.15}+\frac{13}{15.28}\)
\(=\frac{1}{2}-\frac{1}{7}+\frac{1}{7}-\frac{1}{11}+\frac{1}{11}-\frac{1}{14}+\frac{1}{14}-\frac{1}{15}+\frac{1}{15}-\frac{1}{28}\)
\(=\frac{1}{2}-\frac{1}{28}=\frac{13}{28}\)
\(\Rightarrow B=\frac{13}{28}:\frac{1}{7}=\frac{13}{28}.7=\frac{13}{4}\)
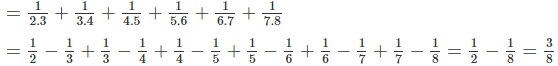
A = 1 2.3 + 2 3.4 + 1 4.5 + 1 5.6 + 1 6.7 + 1 7.8
1 2 − 1 3 + 1 3 − 1 4 + 1 4 − 1 5 + 1 5 − 1 6 + 1 6 − 1 7 + 1 7 − 1 8 = 3 8