Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(f\left(x\right)=\frac{x^2}{2}-4\ln\left(3-x\right)\) trên đoạn \(\left[-2;1\right]\)
Ta có :
\(f'\left(x\right)=x+\frac{4}{3-x}=\frac{-x^2+3x+4}{3-x}=0\Leftrightarrow-x^2+3x+4=0\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}x=-1\in\left[-2;1\right]\\x=4\notin\left[-2;1\right]\end{array}\right.\)
Mà :
\(\begin{cases}f\left(-2\right)=2-4\ln5\\f\left(-1\right)=\frac{1}{2}-8\ln2=\frac{1-16\ln2}{2}\\f\left(1\right)=\frac{1}{2}-4\ln2=\frac{1-8\ln2}{2}\end{cases}\) \(\Rightarrow\begin{cases}Max_{x\in\left[-2;1\right]}f\left(x\right)=\frac{1-8\ln2}{2};x=1\\Min_{x\in\left[-2;1\right]}f\left(x\right)=\frac{1-16\ln2}{2};x=-1\end{cases}\)

Ta có :
\(f'\left(x\right)=2x\ln x-x=x\left(2\ln x-1\right)=0\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}x=0\\\ln x=\frac{1}{2}\ln\sqrt{e}\end{array}\right.\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}x=0\notin\left[\frac{1}{e};e^2\right]\\x=\sqrt{e}\in\left[\frac{1}{e};e^2\right]\end{array}\right.\)
Mà : \(\begin{cases}f\left(\frac{1}{e}\right)=-\frac{1}{e^2}\\f\left(e\right)=\frac{e}{2}\\f\left(e^2\right)=2e^4\end{cases}\) \(\Rightarrow\begin{cases}Max_{x\in\left[\frac{1}{e};e^2\right]}f\left(x\right)=2e^4;x=e^2\\Min_{x\in\left[\frac{1}{e};e^2\right]}f\left(x\right)=\frac{-1}{e^2};x=\frac{1}{e}\end{cases}\)

Xét hàm số f(x) = x 3 + 3 x 2 − 72x + 90 trên đoạn [-5;5]
f′(x) =3 x 2 + 6x − 72;
f′(x) = 0 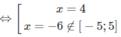
f(−5) = 400; f(5) = −70; f(4) = −86
Ngoài ra, f(x) liên tục trên đoạn [-5;5] và f(−5).f(5) < 0 nên tồn tại x 0 ∈ (−5;5) sao cho f( x 0 ) = 0
Ta có g(x) = |f(x)| ≤ 0 và g( x 0 ) = |f( x 0 )| = 0;
g(−5) = |400| = 400
g(5) = |−70| = 70; g(4) = |f(4)| = |−86| = 86
Vậy min g(x) = g( x 0 ) = 0; max g(x) = g(−5) = 400

Ta có : \(f'\left(x\right)=2x+\frac{2}{1-2x}=\frac{-4x^2+2x+2}{1-2x}=0\Leftrightarrow-4x^2+2x+2=0\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}x=-\frac{1}{2}\in\left[-2;0\right]\\x=1\notin\left[-2;0\right]\end{array}\right.\)
Mà :
\(\begin{cases}f\left(-2\right)=4-\ln5;x=-2\\f\left(-\frac{1}{2}\right)=\frac{1}{4}-\ln2=\frac{1-4\ln2}{4};x=-\frac{1}{2}\\\end{cases}\)
min f(x) = f(1) = 4. Không có giá trị lớn nhất.