Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

câu 4 \(\sqrt{x^2-2x}=\sqrt{2x-x^2}\Leftrightarrow x^2-2x=2x-x^2\)
\(\Leftrightarrow2\left(x^2-2x\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
câu C
Câu 5 \(x\left(x^2-1\right)\sqrt{x-1}=0\)
ĐK \(x\ge1\)
\(\Leftrightarrow\left(x-1\right)\left(x+1\right)\sqrt{x-1}=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x+1=0\\\sqrt{x-1}=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\left(nh\right)\\x=-1\left(l\right)\end{matrix}\right.\)
vậy pt có 1 nghiệm
câu B

\(2\left(x-3\right)\left(x+3\right)\ge0\Rightarrow\left[{}\begin{matrix}x\ge3\\x\le-3\end{matrix}\right.\)
Đáp án D đúng

Câu 1: đáp án B, thay tọa độ A vào pt được \(1\le0\) (sai)
Câu 2: đáp án D
\(\left(m+n\right)^2\ge4mn\Leftrightarrow m^2+n^2+2mn\ge4mn\Leftrightarrow m^2+n^2\ge2mn\)
Câu 3: đáp án D
\(m=x^2+y^2\ge\frac{\left(x+y\right)^2}{2}=\frac{4}{2}=2\)
Câu 4:
\(\Leftrightarrow5x-\frac{2}{5}x>4\Leftrightarrow\frac{23}{5}x>4\Leftrightarrow x>\frac{20}{23}\)
Câu 5:
\(f\left(x\right)>0\Leftrightarrow23x-20>0\Leftrightarrow x>\frac{20}{23}\) đáp án C
Câu 6:
Bạn viết sai đề, nhìn BPT đầu tiên \(2x-5-1>0\) là thấy có vấn đề
Câu 7:
\(3x+2\left(y+3\right)>4\left(x+1\right)-y+3\)
\(\Leftrightarrow x-3y+1< 0\)
Thay tọa độ D vào ta được \(-1< 0\) đúng nên đáp án D đúng
Câu 8:
Thay tọa độ vào chỉ đáp án D thỏa mãn
Câu 9:
Đáp án C đúng
Câu 10:
Đáp án B đúng (do tọa độ x âm ko thỏa mãn BPT đầu tiên)

\(\left(x-1\right)\left(x-3\right)\le\frac{18}{x^2-4x-4}\) ( ĐK : \(\left\{{}\begin{matrix}x\ne2+2\sqrt{2}\\x\ne2-2\sqrt{2}\end{matrix}\right.\) )
\(\Leftrightarrow x^2-4x+3\le\frac{18}{x^2-4x-4}\)
Đặt \(x^2-4x+3=a\)
\(\Leftrightarrow a\le\frac{18}{a-7}\)
\(\Leftrightarrow\frac{a^2-7a-18}{a-7}\le0\)
\(\Leftrightarrow\frac{\left(a+2\right)\left(a-9\right)}{a-7}\le0\)
Lập bảng xét dấu và giải ra ta được :
\(\left[{}\begin{matrix}a\le-2\\7< a\le9\end{matrix}\right.\)
Với \(a\le-2\)
\(\Leftrightarrow x^2-4x+5\le0\) ( Vô nghiệm )
Với \(7< a\le9\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2-4x-4\ge0\\x^2-4x-6\le0\end{matrix}\right.\) \(\Leftrightarrow x\in\) [ \(2-\sqrt{10};2-2\sqrt{2}\) ) \(\cup\) ( \(2+2\sqrt{2};2+\sqrt{10}\) )
\(P=2-2\sqrt{2}+2+2\sqrt{2}=4\)

1.
\(\left\{{}\begin{matrix}x>2\\\frac{5}{2}+3\le x+\frac{3}{2}x\\2x\le5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x>2\\\frac{5}{2}x\ge\frac{11}{2}\\x\le\frac{5}{2}\end{matrix}\right.\) \(\Rightarrow\frac{11}{5}\le x\le\frac{5}{2}\)
\(\Rightarrow a+b=\frac{11}{5}+\frac{5}{2}=D\)
2.
\(\left\{{}\begin{matrix}6x-4x>7-\frac{5}{7}\\4x-2x< 25-\frac{3}{2}\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x>\frac{22}{7}\\x< \frac{47}{4}\end{matrix}\right.\)
\(\Rightarrow\frac{22}{7}< x< \frac{47}{4}\Rightarrow x=\left\{4;5...;11\right\}\) có 8 giá trị
3.
\(\left\{{}\begin{matrix}5x-4x< 5+2\\x^2< x^2+4x+4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x< 7\\x>-1\end{matrix}\right.\)
\(\Rightarrow-1< x< 7\Rightarrow x=\left\{0;1;...;6\right\}\)
\(\Rightarrow\sum x=1+2+...+6=21\)
4.
\(\left\{{}\begin{matrix}x^2-2x+1\le8-4x+x^2\\x^3+6x^2+12x+8< x^3+6x^2+13x+9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x\le7\\x\ge-1\end{matrix}\right.\) \(\Rightarrow-1\le x\le\frac{7}{2}\)
\(\Rightarrow\left\{{}\begin{matrix}x_{min}=-1\\x_{max}=3\end{matrix}\right.\) \(\Rightarrow S=2\)
5.
\(\left\{{}\begin{matrix}x>\frac{1}{2}\\x< m+2\end{matrix}\right.\)
Hệ đã cho có nghiệm khi và chỉ khi:
\(m+2>\frac{1}{2}\Rightarrow m>-\frac{3}{2}\)

a) <=>
Miền nghiệm của hệ bất phương trình là miền không bị gạch sọc ở hình bên (không kể các điểm).
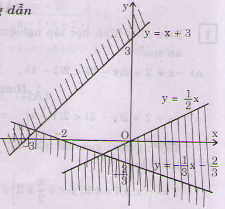
b) <=>
Miền nghiệm của hệ bất phương trình là miền tam giác ABC bao gồm cả các điểm trên cạnh AC và cạnh BC (không kể các điểm của cạnh AB).
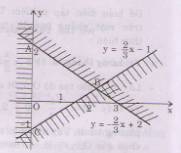

Chọn B.
Ta có:
Tập nghiệm của hệ bất phương trình là S = [-3;3).