K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
VK
22 tháng 4 2017
a) Từ a + 5 < b + 5
=> a + 5 + (-5) < b + 5 + (-5) (cộng hai vế với -5)
=> a < b
8 tháng 4 2021
a)từ a+5<b+5 ta cộng -5 vào 2 vế được a<b
b)từ -3a>-3b ta nhân 2 vế với -1/3 (tức là chia cả 2 vế cho -3) và -3a . -1/3< -3b . -1/3 sẽ được a<b
20 tháng 8 2017
Ta có : 2a + b chia hết cho 13
=> 10a + 5b chia hết cho 13
=> 10a - 8b + 13b chia hết cho 13
=> (10a - 8b) + 13b chia hết cho 13
=> 2(5a - 4b) + 13b chia hết cho 13
Vì 13b chia hết cho 13
Nên : 2(5a - 4b) chia hết cho 13
=> 5a - 4b chia hết cho 13 (đpcm)
ND
27 tháng 3 2018
Bài 1:
a). Ta có: a < b
=> -6a > -6b
mà 3 > 1
=> \(3-6a>1-6b\)
b)
Ta có: a < b
=> a - 2 < b - 2
=> \(7\left(a-2\right)< 7\left(b-2\right)\)
c)
Ta có: a < b
=> -2a > -2b
=> 1 - 2a > 1 - 2b
\(\Rightarrow\dfrac{1-2a}{3}>\dfrac{1-2b}{3}\)
NT
1
25 tháng 9 2019
\(A=\sqrt{6+\sqrt{6+\sqrt{6}}}+\sqrt{2+\sqrt{2+\sqrt{2}}}\)
\(A< \sqrt{6+\sqrt{6+\sqrt{9}}}+\sqrt{2+\sqrt{2+\sqrt{4}}}\)
\(=\sqrt{6+\sqrt{6+3}}+\sqrt{2+\sqrt{2+2}}\)
\(=\sqrt{6+\sqrt{9}}+\sqrt{2+\sqrt{4}}\)
\(=\sqrt{6+3}+\sqrt{2+2}\)
\(=\sqrt{9}+\sqrt{4}\)
\(=3+2=5=B\)
Vậy A < B
Chúc bạn học tốt !!!
NA
0
TT
2
6 tháng 8 2020
\(\left(5a-3b+8c\right)\left(5a-3b-8c\right)=\left(3a-5b\right)^2\)
\(\Leftrightarrow\left(5a-3b\right)^2-64c^2-\left(3a-5b\right)^2=0\)
\(\Leftrightarrow\left(5a-3b-3a+5b\right)\left(5a-3b+3a-5b\right)=64c^2\)
\(\Leftrightarrow\left(2a+2b\right)\left(8a-8b\right)=16\left(a^2-b^2\right)\)
\(\Leftrightarrow16\left(a^2-b^2\right)=16\left(a^2-b^2\right)\left(true\right)\)
Vậy \(\left(5a-3b+8c\right)\left(5a-3b-8c\right)=\left(3a-5b\right)^2\)khi \(a^2-b^2=4c^2\)
NY
6 tháng 8 2020
(5a−3b+8c)(5a−3b−8c)(5a-3b+8c)(5a-3b-8c)
=(5a−3b)2−(8c)2=(5a-3b)2-(8c)2
=(5a−3b)2−16.4c2=(5a-3b)2-16.4c2
Thay a2−b2=4c2a2-b2=4c2 ta có :
=25a2−30ab+9b2−16(a2−b2)=25a2-30ab+9b2-16(a2-b2)
=25a2−30ab+9b2−16a2+16b2=25a2-30ab+9b2-16a2+16b2
=9a2−30ab+25b2=9a2-30ab+25b2
=(3a−5b)2(đpcm)=(3a-5b)2(dpcm)
VL
0
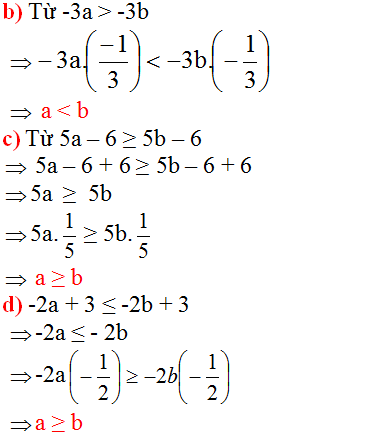
5a – 6 ≥ 5b – 6
⇒ 5a – 6 + 6 ≥ 5b – 6 + 6 (Cộng hai vế với 6)
⇒ 5a ≥ 5b
⇒ a ≥ b (Nhân cả hai vế cho 1/5 > 0, BĐT không đổi chiều).