Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nhiệt lượng mà nước nhận được làm cho nó nóng lên được tính theo công thức:
Q = cm(t2 – t1) = 4 200.2.(80 – 20) = 504000J.
Nhiệt lượng này do dòng điện tạo ra và truyền cho nước, vậy có thể nói rằng, dòng điện có năng lượng, gọi là điện năng. Chính điện năng này đã chuyển hóa thành nhiệt năng làm nước nóng lên. Áp dụng định luật bảo toàn năng lượng cho các hiện tượng nhiệt và điện, ta có thể nói phần điện năng mà dòng điện đã truyền cho nước là 504000J.

- Tính được điện trở cuả dây xoắn là:
\(R=p\frac{l}{s}=5,4.10^{-4}.\frac{10}{0,2.10^{-6}}=27\left(\Omega\right)\)
- Cường độ dòng điện qua bếp : I = \(I=\frac{U}{R}=\frac{220}{27}=8,14\left(A\right)\)
- Tính được nhiệt lượng cần cho nước đã cho đến sôi(Q hữu ích):
Q = cm(t2 – t1) = 4200 J/kg.K.2kg.(100 -15) = 714000J
- Do bếp có hiệu suất nên nhiệt lượng bếp phải cấp :
\(H=\frac{Qi}{Q}.100\%\)80% =>\(Q=\frac{Qi.100\%}{H}=\frac{71400.100\%}{80\%}=892500\left(J\right)\)
- Nhiệt lượng này do điện năng chuyển thành từ dây xoắn. Vậy thời gian cần thiết cho nước sôi :
Q = A = U.I.t = >t = \(\frac{Q}{UI}=\frac{892500}{220.8,14}=497,8\left(s\right)\) = 8,3(phút)
cái đáp án điện trở có phải sai rồi không ? Tôi bấm máy nó lại ra 27000 ohm ấy

\(=>Qthu=mc\Delta t=4200.m\left(100-23\right)=323400m\left(J\right)\)
\(=>Qtoa=I^2Rt=3^2.100.900=810000J\)
\(=>Qthu=Qtoa=>m=2,5kg\)

a/ Từ V = 2 lít → m = 2kg
Nhiệt lượng cần cung cấp cho nước:
Q = m.c.Δt = 2.4200.(100 - 25) = 630000 J
b/ Từ 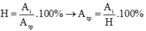
Nhiệt lượng do bếp tỏa ra là:
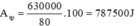
Mặt khác lại có:
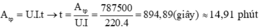
c/ Khi gập đôi dây điện trở của bếp thì điện trở của bếp thì
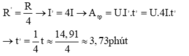

Tóm tắt : \(m=2kg\)
\(t_1=20^{\circ}C\)
\(t_2=80^{\circ}C\)
\(C=4200J/kg.K\)
\(A=?\)
Bài giải :
Nhiệt lượng tỏa ra của dòng điện :
\(Q=m.c.\Delta t\)
\(\Rightarrow A=Q=4200.2\left(80-20\right)=504000\left(J\right)\)
Đáp số : \(A=504000J\)

a. \(Q_{toa}=A=I^2Rt\)
\(Q_{thu}=mc\Delta t=0,5\cdot4200\cdot80=168000\left(J\right)\)
\(Q_{thatthoat}=\dfrac{1}{4}Q_{thu}=\dfrac{1}{4}168000=42000\left(J\right)\)
Theo ĐLBTNL: \(Q_{toa}=Q_{thu}+Q_{thatthoat}=168000+42000=210000\left(J\right)\)
\(Q_{toa}=A=Pt\Rightarrow P=\dfrac{Q_{toa}}{t}=\dfrac{210000}{10\cdot60}=350\)W
b. \(Q_{toa}=Q'_{toa}\Leftrightarrow I^2Rt=I'^2Rt'\)
\(\Rightarrow\dfrac{I^2}{I'^2}=\dfrac{t'}{t}=\dfrac{\left(1\cdot3600\right)+\left(30\cdot60\right)}{10\cdot60}=900\)
\(\Rightarrow I^2=9I'^2=9\)
\(\Rightarrow I=3A\)
c. \(P=I^2R\Rightarrow R=\dfrac{P}{I^2}=\dfrac{350}{9}\approx38,9\Omega\)
Nhiệt lượng do nửa lít nc hấp thụ:
\(Q=mc\Delta t=0,5\cdot4200\cdot\left(100-20\right)=168000J\)
Nhiệt lượng thất thoát:
\(Q'=\dfrac{1}{4}Q=\dfrac{1}{4}\cdot168000=42000J\)
Định luật bảo toàn nhiệt lượng:
\(Q=168000+42000=210000J\)
Công suất tỏa nhiệt:
\(P=RI^2=\dfrac{Q}{t}=\dfrac{210000}{10\cdot60}=350W\)

C1: Hãy tính điện năng A của dòng điện chạy qua dây điện trở trong thời gian trên.
Trả lời:
+ Điện năng A = I2Rt = (2,4)2.5.300 = 8640 J.
C2: Hãy tính nhiệt lượng Q mà nước và bình nhôm nhận được trong thời gian đó.
Trả lời:
+ Nhiệt lượng Q mà nước và bình nhôm nhận được: Q = Q1 + Q2 ; trong đó
Nhiệt lượng nước nhận được Q1 = c1m1 ∆to = 4200.0,2.9,5 = 7980 J.
Nhiệt lượng bình nhôm nhận được Q2 = c2m2 ∆to = 880.0,078.9,5 = 652 J.
Vậy Q = 7980 + 652 = 8632 J.
C3: Hãy so sánh A với Q và nêu nhận xét, lưu ý rằng có một phần nhỏ nhiệt lượng truyền ra môi trường xung quanh.
Trả lời:
+ So sánh: ta thấy A lớn hơn Q một chú. Điện năng tiêu thụ đã có một ít biến thành nhiệt lượng được truyền ra môi trường xung quanh.

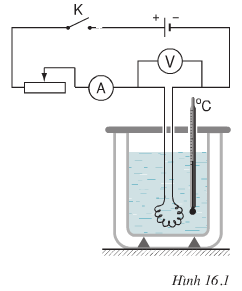
Nhiệt lượng mà nước nhận được làm cho nước nóng lên tính theo công thức:
Q = m.c.(t2 - t1) = 2.4200.(80 - 20) = 504000J.
Nhiệt lượng này do dòng điện tạo ra và truyền cho nước, vậy có thể nói rằng dòng điện có năng lượng, gọi là điện năng. Chính điện năng này đả chuyển thành nhiệt năng làm nước nóng lên.
Áp dụng định luật bảo toàn năng lượng cho các hiện tượng nhiệt và điện, ta có thể nói phần điện năng mà dòng điện đã truyền cho nước là 504000J.