Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Viết phương trình dao động của vật
ω = 2 π /T = π /2 rad/s
Tại t = 0 vật ở biên âm nên ta có x = Acos φ = -A ⇒ cos φ = -1 ⇒ φ = π
Phương trình dao động của vật là x = 24cos( π t/2 + π )(cm)

Tai thời điểm t = 0,5s ta có
Li độ: x = 24.cos( π .0,5/2 + π ) = 24cos5 π /4 = -16,9 ≈ 17 cm
Vận tốc : v = - 24. π /2.sin( π .0,5/2 + π ) = -24.π/2.sin5 π /4 = 6 π 2 cm/s = 26,64 cm/s ≈ 27 cm/s
Gia tốc : a = - π / 2 2 .x = - π / 2 2 .(-16,9) = 41,6 cm/ s 2 ≈ 42 (cm/ s 2 )

Thời điểm đầu tiên vật đi qua li độ x = -12 cm là
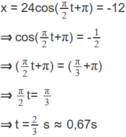
Tốc độ tại thời điểm t = 2/3s là:
v = - ω Asin( π /3 + π ) = 32,6 cm/s ≈ 33 cm/s

Áp dụng: \(v_{max} = \omega A \Rightarrow A = \frac{v_{max}}{\omega} = 120/20 =6 \ cm\)
Li độ trễ pha \(\frac {\pi}{2}\) so với vận tốc, nên ta có phương trình dao động là: \(x = 6\cos(10 t - \frac{\pi}{2}) \ (cm)\)
Thay t = T/6 vào phương trình trên, ta được x = \(3\sqrt3 \ cm\)

Khoảng thời gian vận tốc của vật không vượt quá \(6\pi cm/s\) là \(\frac{\Delta t}{T}=\frac{1}{3}\)
\(\Rightarrow\)Góc quét: \(\Delta\varphi=\frac{2\pi}{T}\frac{T}{3}=\frac{2\pi}{3}\left(rad\right)\)
\(\Rightarrow\) VTLG
-v
\(\Rightarrow\cos\varphi=\cos\left(90-30\right)=\frac{v}{v_{max}}=\frac{1}{2}\Rightarrow v_{max}=12\pi=\)\(\omega A\Rightarrow A=3,6cm\)

Thời điểm đầu tiên vật qua vị trí có li độ x = -12 cm

Tốc độ của vật tại thời điểm t = 2/3 s
![]()
⇒ v ≈ 0,33 m/s

Tại thời điểm t = 0,5s ta có
Li độ của vật là : x = 24cos5 π /4 = 24.(- 2 /2) = -16,9cm ≈ -17cm
Gia tốc của vật là : a = - ω 2 x = - π / 2 2 .(-16,9) = 42cm/ s 2
Lực kéo về là : F = ma ≈ 0,01.0,42 = 0,0042N

Đáp án A
Hai thời điểm vuông pha nhau, ta có A = x 1 2 + x 2 2 = 5
Viết phương trình dao động của vật
A = 24cm; T= 4s ⇒ ω = 2 π /T = π /2; Tại thời điểm ban đầu vật ở biên âm nên ta có φ = π
Nên phương trình dao động của vật là : x = 24cos( π t/2 + π ).