Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D.
Sô cách lấy bằng số cách chọn ra 6 quyển để bỏ lại. Yêu cầu đặt ra là 6 quyển để lại phải đủ cả 3 môn.
TH1: 1 văn, 2 âm nhạc, 3 hội họa: C 5 1 . C 4 2 . C 3 3
TH2: 1 văn, 3 âm nhạc, 2 hội họa: C 5 1 . C 4 3 . C 3 2
TH3: 1 văn, 4 âm nhạc, 1 hội họa: C 5 1 . C 4 4 . C 3 1
TH4: 2 văn, 1 âm nhạc, 3 hội họa: C 5 2 . C 4 1 . C 3 3
TH5: 2 văn, 2 âm nhạc, 2 hội họa: C 5 2 . C 4 2 . C 3 2
TH6: 2 văn, 3 âm nhạc, 1 hội họa: C 5 2 . C 4 3 . C 3 1
TH7: 3 văn, 1 âm nhạc, 2 hội họa: C 5 3 . C 4 1 . C 3 2
TH8: 3 văn, 2 âm nhạc, 1 hội họa: C 5 3 . C 4 2 . C 3 1
TH9: 4 văn, 1 âm nhạc, 1 hội họa: C 5 4 . C 4 1 . C 3 1
Lấy 6 quyển sách chia cho 6 bạn: 6! = 720
Nhân lại ta có : 579600 cách

Không gian mẫu là số cách chọn ngẫu nhiên 5 trong 10 cuốn sách rồi tặng cho 5 học sinh.
Suy ra số phần tử của không gian mẫu là ![]() .
.
Gọi A là biến cố Sau khi tặng sách thì mỗi một trong ba loại sách của thầy giáo còn lại ít nhất một cuốn .
Để tìm số phần tử của A, ta tìm số phần tử của biến cố ![]() , tức sau khi tặng sách có môn không còn lại cuốn nào.
, tức sau khi tặng sách có môn không còn lại cuốn nào.
Vì tổng số sách của hai loại bất kỳ lớn hơn 5 cuốn nên không thể chọn sao cho cùng hết 2 loại sách. Do vậy chỉ có thể một môn hết sách, ta có các khả năng:
Cách tặng sao cho không còn sách Toán, tức là ta tặng 4 cuốn sách toán, 1 cuốn còn lại Lý hoặc Hóa
+) 4 cuốn sách Toán tặng cho 4 người trong 5 người, có ![]() cách.
cách.
+) 1 người còn lại được tặng 1 cuốn trong 6 cuốn (Lý và Hóa), có ![]() .
.
Suy ra có ![]() cách tặng sao cho không còn sách Toán.
cách tặng sao cho không còn sách Toán.
Tương tự, có ![]() cách tặng sao cho không còn sách Lý.
cách tặng sao cho không còn sách Lý.
Tương tự, có ![]() cách tặng sao cho không còn sách Hóa.
cách tặng sao cho không còn sách Hóa.
Suy ra số phần tử của biến cố ![]() là.720+2520+2520=5760
là.720+2520+2520=5760
Suy ra số phần tử của biến cố A là.30240-5760=24480
Vậy xác suất cần tính 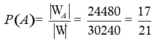
Chọn C.

Chọn C
Xét phép thử T: “Chọn 7 cuốn sách từ 15 cuốn sách”.
Số phần tử của không gian mẫu trong phép thử là C 15 7 .
Gọi A biến cố chọn 7 cuốn sách có đủ 3 môn trong phép thử T.
Xác suất của biến cố cần tìm bằng xác suất của biến cố A.
Ta có ![]()
Vậy
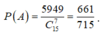

a) Số cách chọn 6 quyển sách Toán và Văn là:\(C^1_5.C^5_6+C^2_5.C^4_6+C^3_5.C^3_6+C^4_5.C_6^2+C^5_5.C^1_6=321\)(cách)
Tương tự: Có 1708 cách chọn 6 quyển sách Anh và Văn
Có: 917 cách chọn 6 quyển sách Toán và Anh
-> Có 2946 cách

Đáp án B

Gọi biến cố A: “Số cuốn sách còn lại của thầy Tuấn có đủ cả ba môn”.
Khi đó ta có biến cố: A ¯ : “Số cuốn sách còn lại của thầy Tuấn không có đủ cả 3 môn”.


Số cách tặng 6 quyển sách tuỳ ý là: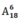
Số cách tặng hết sách lí 5!.13 = 1560
Số cách tặng hết sách hoá: 6! = 720
Số cách tặng thỏa yêu cầu bài toán: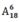 -1560 - 720 = 13363800
-1560 - 720 = 13363800
Chọn C