Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
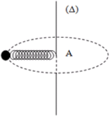
Lực đàn hồi của lò xo đóng vai trò là lực hướng tâm.
Khi trục Δ quay thì lò xo giãn ra một đoạn ∆ℓ.
Fht = Fdh ↔ mω2(ℓo + ∆ℓ) = k.∆ℓ → (k – mω2).∆ℓ = mω2ℓo


Đáp án A
Lực đàn hồi của lò xo đóng vai trò là lực hướng tâm.
Khi trục Δ quay thì lò xo giãn ra một đoạn Δ l
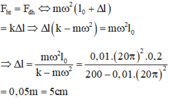

Chọn A
Lực đàn hồi của lò xo đóng vai trò là lực hướng tâm.
Khi trục quay thì lò xo giãn ra một đoạn Δl
F h t = F d h ↔ m ω 2 ( l 0 + Δℓ) = k.Δℓ → (k – m ω 2 ).Δℓ = m ω 2 l 0
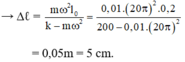

Ta có: ω = 2 π f = 2 π 360 60 = 12 π
Lực đàn hồi của lò xo đóng vai trò là lực hướng tâm:
Khi trục Δ quay thì lò xo dãn một đoạn Δl
→ F h t = F d h ↔ m ω 2 ( l 0 + Δ l ) = k Δ l → Δ l ( k − m ω 2 ) = m ω 2 l 0 → Δ l = m ω 2 l 0 k − m ω 2 = 0 , 01. ( 12 π ) 2 0 , 4 125 − 0 , 01. ( 12 π ) 2 = 0 , 0513 m = 5 , 13 c m
Đáp án: C

Theo bài ra ta có:
W=Wđ+Wt =1/2.m.v2 +1/2.k.x2= 5.1/2.k.x2
Khi wt =4wđ thì cơ năng ở đó là:
w=wđ+wt = 5/4.wt = 5/4.1/2.kx'2
Theo định luật bảo toàn cơ năng cho hai vị trí ta có:
5/4.1/2.kx'^2 = 5.1/2.k.x^2 -> x' = ...

\(\overrightarrow{F_{ht}}=m.\overrightarrow{a_{ht}}\Rightarrow F_{ht}=m.a_{ht}\)
\(\overrightarrow{F_{msn}}=\mu.\overrightarrow{N}\Rightarrow F_{msn}=\mu mg\)
Có \(F_{ht}\le F_{msn}\Rightarrow m.a_{ht}\le\mu mg\)
\(\Leftrightarrow\omega^2.R\le\pi^2.\mu\)
\(\Leftrightarrow\pi^2.0,2\le\pi^2.\mu\Rightarrow\mu\ge0,2\)
Vậy để vât ko bị trượt thì \(\mu\ge0,2\)

45 P N F dh
Chọn trục toạ độ như hình vẽ.
Vật ở VTCB lò xo bị nén \(\Delta \ell_0\)
Vật đang đứng yên ở VTCB, hợp lực tác dụng lên vật bằng 0
\(\Rightarrow \vec{P}+\vec{F_{dh}}+\vec{N}=\vec{0}\)
Chiếu lên trục toạ độ ta được: \(P.\sin 45^0-F_{dh}=0\)
\(\Rightarrow mg.\sin 45^0=k.\Delta \ell_0\)
\(\Rightarrow k=\dfrac{mg.\sin 45^0}{\Delta \ell_0}=\dfrac{0,2.10.\sin 45^0}{0,02}=50\sqrt 2(N/m)\)
Chọn C.

 10
10
Chọn đáp án A
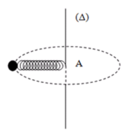
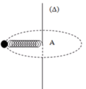
Lực đàn hồi của lò xo đóng vai trò là lực hướng tâm.
Khi trục ∆ quay thì lò xo giãn ra một đoạn ∆ℓ.
Fht = Fdh
<-> mω2(ℓo + ∆ℓ) = k.∆ℓ
→ (k – mω2).∆l = mω2ℓo