Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Gọi u1là số tiền phải trả cho 10 số điện đầu tiên. u 1 = 10.800 = 8000 (đồng)
u2 là số tiền phải trả cho các số điện từ 11 đến 20: u 2 = u 1 1 + 0 , 025
u3 là số tiền phải trả cho các số điện từ 331 đến 340: u 34 = u 1 1 + 0.025 33
Số tiền phải trả cho 340 số điện đầu tiên là: S 1 = u 1 = 1 − 1 + 0 , 025 34 1 − 1 + 0 , 025 = 420903 , 08
Số tiền phải trả cho các số điện từ 341 đến 347 là: S 2 = 7.800 1 + 0 , 025 34 = 12965 , 80
Vậy tháng 1 gia đình ông A phải trả số tiền là: S = S 1 + S 2 = 433868 , 89 đồng.

Độ cao của các bậc thang thứ n của tòa nhà được tính theo công thức: u = 0 , 95 + n - 1 . 0 , 15 .
Độ cao của bậc thứ 8 so với mặt đất là: u 8 = 0 , 95 + 7 . 0 , 15 = 2
Chọn B.

Đáp án D.
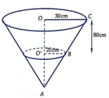
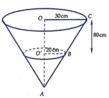
Xét hình nón đỉnh A, đường cao h(h > 80cm) và có đáy là đường tròn tâm O, bán kính R = 30cm. Mặt phẳng cách mặt đáy 80 cm và cắt hình nón theo giao tuyến là đường tròn tâm O' có bán kính r = 20cm. Mặt phẳng chia hình nón thành 2 phần. Phần (I) là phần chứa đỉnh A, phần (II) là phần không chứa đỉnh A (hình vẽ).
Ta có O ' B O C = A O ' A O ⇔ A O ' A O ' + O ' O = 2 3 ⇔ A O ' A O ' + 80 = 2 3 ⇔ A O ' = 160 ( c m )
Thể tích hình nón là V = 1 3 A O . πR 2 = 1 3 160 + 80 . π . 30 2 = 72000 π ( cm 3 )
Thể tích phần (I) là V I = 1 3 A O ' . πr 2 = 1 3 160 π . 20 2 = 64000 3 π ( cm 3 )
Thể tích cái xô cũng là thể tích phần (II), ta có :
V ( I I ) = V - V ( I ) = 72000 π - 64000 3 π = 152000 3 π ( cm 3 ) = 19 375 π ( m 3 )
Vậy số tiền phải trả mỗi tháng là
20000 . V I I . 10 = 20000 . 19 375 π . 10 ≈ 31835 (đồng).

Đáp án D
Số tiền phải trả hằng tháng bằng 96.1 % . 1 + 1 % 24 1 + 1 % 24 − 1 ≈ 4 , 52 triệu đồn

Nếu trong 11 số tự nhiên đó có 1 số chia hết cho 10 thì bài toán đã được chứng minh.
Nếu trong 11 số đã cho, không có số nào chia hết cho 10, ta đặt:
A1= 1
A2= 1+2
A3= 1+2+3
...
A11= 1+2+3+...+10+11
Ta biết rằng, trong 1 phép chia cho 10, ta luôn nhận được 10 số dư từ 0->9
Vì ta có 11 dãy số nên ít nhất có 2 dãy số có cùng số dư trong phép chia cho 10.
Giả sử, dãy Bm và Bn có cùng số dư trong phép chia cho 10 thì ( Bm - Bn ) chia hết cho 10. => đpcm.

Đáp án B
Gọi A là số tiền gốc ban đầu, lãi suất r/năm, số tiền gửi thêm là a (triệu đồng)
Sau năm đầu tiên, số tiền cả gốc lẫn lãi mà ông Minh nhận đc là A(1+r)
Sau năm thứ 2, cả gốc và lãi ông nhận được là
![]()
Sau năm thứ 3, cả gốc và lãi ông nhận được:
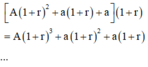
Sau năm thứ n, ông Minh nhận được số tiền:
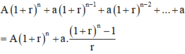
Thay số: sau 10 năm ông Minh nhận về cả gốc lẫn lãi là
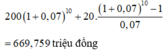
Đáp án B
Gọi A là số tiền gốc ban đầu, lãi suất r/năm, số tiền gửi thêm là a (triệu đồng)
Sau năm đầu tiên, số tiền cả gốc lẫn lãi mà ông Minh nhận đc là A(1+r)
Sau năm thứ 2, cả gốc và lãi ông nhận được là
![]()
Sau năm thứ 3, cả gốc và lãi ông nhận được:
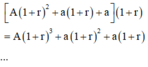
Sau năm thứ n, ông Minh nhận được số tiền:
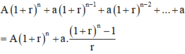
Thay số: sau 10 năm ông Minh nhận về cả gốc lẫn lãi là
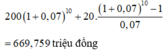

Đáp án C
Gọi A là số tiền gốc ban đầu, lãi suất r / năm, số tiền gửi thêm là a (triệu đồng).
Sau năm đầu tiên, số tiền cả gốc lẫn lãi mà ông Minh nhận được là: A 1 + r
Sau năm thứ 2, cả gốc và lãi ông nhận được là: A 1 + r + a 1 + r = A 1 + r 2 + a 1 + r
Sau năm thứ 3, cả gốc và lãi ông nhận được:
A 1 + r 2 + a 1 + r + a 1 + r = A 1 + r 3 + a 1 + r 2 + a 1 + r
…
Sau năm thứ n, ông Minh nhận được số tiền:
A 1 + r n + a 1 + r n − 1 + a 1 + r n − 2 + . .. + a = A 1 + r n + a . 1 + r n − 1 r
Thay số: sau 10 năm ông Minh nhận về cả gốc lẫn lãi là
200 1 + 0 , 07 10 + 20. 1 + 0 , 07 10 − 1 0 , 07 = 669 , 759 triệu đồng.
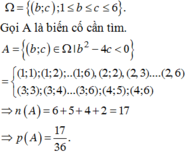
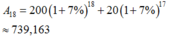
Đáp án B
Ta phân tích 847 - 840 + 7 = 84.10 + 7 suy ra có 84 bậc số điện. Số tiền ông A phải trả cho bậc 1 là 10.500 đồng.
Số tiền ông A phải trả cho bậc 2 là 10.(500 + 500.2,5%) đồng.
Số tiền ông A phải trả cho bậc 3 là 10.[500.(1 + 2,5%) + 500.(1 + 2,5%).2,5%] = 10.500. 1 , 025 2 đồng.
… … …
Số tiền ông A phải trả cho bậc 84 là 10 . 500 . 1 , 025 83 đồng.
Vậy tổng số tiền ông A phải trả là T = 5000 + 5000 . 1 , 025 + . . . + 5000 . 1 , 025 83 + 7 . 500 . 1 , 025 84 .
Xét cấp số nhân có u 1 = 1 ; u n = 1 , 025 83 và q = 1 , 025 ⇒ S = 1 + 1 , 025 + 1 , 025 2 + . . . + 1 , 025 83 = u 1 . 1 - q n 1 - q
Suy ra S = 1 - 1 , 025 84 1 - 1 , 025 . Vậy T = 5000 . 1 - 1 , 025 84 1 - 1 , 025 + 7 . 500 . 1 , 025 84 ≈ 1419455 , 83 . .