Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
+ Ban đầu M là vân tối thứ 3 nên: \(x_M=\left(2+\frac{1}{2}\right)\frac{\lambda D}{a}\left(1\right)\)
+ Khi giãm S1S2 một lượng \(\Delta\)a thì M là vân sáng bậc n nên: \(x_M=n\frac{\lambda D}{a-\Delta a}\left(2\right)\)
+ Khi tăng S1S2 một lượng \(\Delta\)a thì M là vân sáng bậc 3n nên: \(x_M=3n\frac{\lambda D}{a+\Delta a}\left(3\right)\)
+ (2) và (3) \(\Rightarrow k\frac{\lambda D}{a-\Delta a}=3k\frac{\lambda d}{a+\Delta a}\Rightarrow\Delta a=\frac{a}{2}\)
+ Khi tăng S1S2 một lượng 2\(\Delta\)a thì M là sáng bậc k nên: \(x_M=k\frac{\lambda D}{a+2\Delta a}=2,5\frac{\lambda D}{a}\left(4\right)\)
+ Từ (1) và (4) \(\Rightarrow\) k = 5. Vậy tại M lúc này là vân sáng bậc 5.
Sử sụng hệ thức: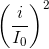 
+
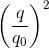= 1
Thay số và giải hệ phương trình trìm I0 và q0
Tần số góc: ω =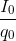 
= 50 (rad/s)
Khoảng cách giữa 2 vân sáng gần nhau nhất cùng màu với vân trung tâm: \(x_T=k_1i_1=k_2i_2\)(1)
\(\Rightarrow k_1\lambda_1=k_2\lambda_2\Rightarrow\frac{k_1}{k_2}=\frac{\lambda_2}{\lambda_1}=\frac{0,6}{0,48}=\frac{5}{4}\)
\(\Rightarrow\begin{cases}k_1=5\\k_2=4\end{cases}\)
Thay vào (1) \(x_T=5i_1=4i_2\)
Như vậy tại vị trí 2 vân trùng nhau kể từ vân trung tâm có vân bậc 5 của \(\lambda_1\) và bậc 4 của \(\lambda_2\)
Do đó, giữa 2 vân sáng cùng màu vân trung tâm có: 4 vân sáng λ1 và 3 vân sáng λ2.
Đáp án A.
\(i_1 = \frac{\lambda_1D_1}{a}\)
\(i_2 = \frac{\lambda_2D_2}{a}\)
=> \(\frac{i_1}{i_2} = \frac{\lambda_1D_1}{\lambda_2D_2} \)
=> \(\frac{\lambda_1}{\lambda_2} = \frac{i_1D_2}{i_2D_1} = \frac{1.2}{3.1}= \frac{2}{3}\) (do \(i_2 = 3i_1; D_2 = 2D_1\))
=> \(\lambda_2 = \frac{3\lambda_1}{2} = \frac{3.0,4}{2} = 0,6 \mu m.\)
Chọn đáp án.A
Hướng dẫn:
\(U_{AB}=U_C=2\) (1)
\(U_{BC}^2=U_r^2+U_L^2=3\) (2)
\(U_{AC}^2=U_r^2+(U_L-U_C)^2=1\) (3)
Giải hệ 3 pt trên sẽ tìm đc \(U_r\) và \(U_L\)
Chia cho \(I\) sẽ tìm được \(r\) và \(Z_L\)
Ta có: \(\begin{cases}\Delta l_1=l_1-l_0=\frac{g}{\omega^2_1}\\\Delta l_2=l_2-l_0=\frac{g}{\omega^2_2}\end{cases}\)\(\Rightarrow\frac{\omega^2_2}{\omega^2_1}=\frac{21-l_0}{21,5-l_0}=\frac{1}{1,5}\)\(\Rightarrow l_0=20\left(cm\right)\)
\(\Rightarrow\Delta l_1=0,01\left(m\right)=\frac{g}{\omega^2_1}\Rightarrow\omega_1=10\pi\left(rad/s\right)\)
KQ = 3,2 cm
Khi tăng điện dung nên 2.5 lần thì dung kháng giảm 2.5 lần. Cường độ dòng trễ pha hơn hiệu điện thế $\pi/4$ nên
$Z_L-\frac{Z_C}{2.5}=R$
Trường hợp đầu tiên thì thay đổi C để hiệu điện thế trên C cực đại thì $Z_LZ_C=R^2+Z_L^2$
$Z_LZ_C=(Z_L-\frac{Z_C}{2.5})^2+Z_L^2$
Giải phương trình bậc 2 ta được: $Z_C=\frac{5}{4}Z_L$ hoặc $Z_C=10Z_L$(loại vì Zl-Zc/2.5=R<0)
$R=\frac{Z_L}{2}$
Vẽ giản đồ vecto ta được $U$ vuông góc với $U_{RL}$ còn $U_C$ ứng với cạch huyền
Góc hợp bởi U và I bằng với góc hợp bởi $U_L$ và $U_{LR}$
$\tan\alpha=\frac{R}{Z_L}=0.5$
$\sin\alpha=1/\sqrt5$
$U=U_C\sin\alpha=100V$
\(U_{C}{max}=\frac{U\sqrt{R^{2}+Z_L^{2}}}{R}\); \(Zc=\frac{R^{2}+Z_L^{2}}{Z_L}\)
khi C2=2,5C1---->Zc2=Zc1/2,5=ZC/2,5
do i trể pha hơn U nên Zl>Zc/2,5
\(\tan\frac{\pi }{4}=\frac{Z_L-0,4Zc}{R}=1\Rightarrow R=Z_L-0,4Z_C\)
\(\Rightarrow Z_C.Z_L=Z_L^{2}+(Z_L-0,4Z_C)^{2}\Rightarrow 2Z_L^{2}-1,8Z_CZ_L+0,16Z_C^{2}=0\Rightarrow Z_L=0,8Z_C;Z_L=0,1Z_C\)(loai)
\(\Rightarrow R=Z_L-1,25.0,4Z_L=0,5Z_L\)
\(\Rightarrow U_{C}{max}=\frac{U\sqrt{Z_L^{2}+0,25Z_L^{2}}}{0,5Z_L}=100\sqrt{5}\Rightarrow U=100V\)
\(x_s= k\frac{\lambda D}{a}.\)
\(d_2-d_1 = \frac{x_sa}{D}= k\lambda\)
=>\(k= \frac{d_2-d_1}{\lambda}=\frac{1,5.10^{-6}}{\lambda}.(1)\)
Thay các giá trị của bước sóng \(\lambda\)1, \(\lambda\)2,\(\lambda\)3 vào biểu thức (1) làm sao mà ra số nguyên thì đó chính là vân sáng của bước sóng đó.
Ta có công thức:
\(n=a+\dfrac{b}{\lambda^2}\), trong đó a,b là các hằng số phụ thuộc môi trường.
Lập hệ pt \(\Rightarrow\left\{{}\begin{matrix}a=1,484\\b=8,944.10^{-15}\end{matrix}\right.\)
thay số \(\Rightarrow n_{vàng}=a+\dfrac{b}{\left(\lambda_{vàng}\right)^2}=1,484+\dfrac{8,944.10^{-15}}{\left(0,58.10^{-6}\right)^2}=1,51\)
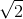
Đáp án D
Bước sóng càng lớn thì chiết suất càng nhỏ nên chiết suất của lăng kính với các ánh sáng: n 2 > n 1 > n 3