
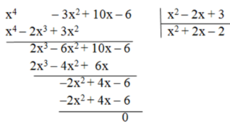
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

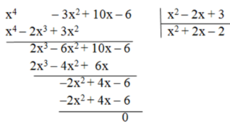

a: \(\Leftrightarrow x\left(16-x^2\right)+x^3-125=3\)
=>16x-125=3
=>16x=128
hay x=8
b: \(\Leftrightarrow x^3+3x^2+3x+1-x^3+3x^2-3x+1-6\left(x^2-2x+1\right)=-10\)
\(\Leftrightarrow6x^2+2-6x^2+12x-6=-10\)
=>12x-4=-10
=>12x=-6
hay x=-1/2
c: \(\Leftrightarrow x^3-27+x\left(4-x^2\right)=1\)
\(\Leftrightarrow4x-27=1\)
hay x=7

c: \(=\dfrac{1}{3x-2}-\dfrac{4}{3x+2}+\dfrac{3x-6}{\left(3x-2\right)\left(3x+2\right)}\)
\(=\dfrac{3x+2-12x+8+3x-6}{\left(3x-2\right)\left(3x+2\right)}\)
\(=\dfrac{-6x+4}{\left(3x-2\right)\left(3x+2\right)}=\dfrac{-2}{3x+2}\)
d: \(=\dfrac{x^2-4-x^2+10}{x+2}=\dfrac{6}{x+2}\)
e: \(=\dfrac{1}{2\left(x-y\right)}-\dfrac{1}{2\left(x+y\right)}-\dfrac{y}{\left(x-y\right)\left(x+y\right)}\)
\(=\dfrac{x+y-x+y-2y}{2\left(x-y\right)\left(x+y\right)}=0\)

1.
\(\frac{2x+3}{4}-\frac{5x+3}{6}=\frac{3-4x}{12}\)
\(MC:12\)
Quy đồng :
\(\Rightarrow\frac{3.\left(2x+3\right)}{12}-\left(\frac{2.\left(5x+3\right)}{12}\right)=\frac{3x-4}{12}\)
\(\frac{6x+9}{12}-\left(\frac{10x+6}{12}\right)=\frac{3x-4}{12}\)
\(\Leftrightarrow6x+9-\left(10x+6\right)=3x-4\)
\(\Leftrightarrow6x+9-3x=-4-9+16\)
\(\Leftrightarrow-7x=3\)
\(\Leftrightarrow x=\frac{-3}{7}\)
2.\(\frac{3.\left(2x+1\right)}{4}-1=\frac{15x-1}{10}\)
\(MC:20\)
Quy đồng :
\(\frac{15.\left(2x+1\right)}{20}-\frac{20}{20}=\frac{2.\left(15x-1\right)}{20}\)
\(\Leftrightarrow15\left(2x+1\right)-20=2\left(15x-1\right)\)
\(\Leftrightarrow30x+15-20=15x-2\)
\(\Leftrightarrow15x=3\)
\(\Leftrightarrow x=\frac{3}{15}=\frac{1}{5}\)

\(\frac{x^2-36}{2x+10}\cdot\frac{3}{6-x}=\frac{\left(x-6\right)\left(x+6\right)}{2x+10}\cdot\frac{3}{6-x}=-\frac{3\left(x+6\right)}{2x+10}=-\frac{3x+18}{2x+10}\)
\(\frac{x^2-4}{x^2-9}\cdot\frac{3x+9}{x+2}=\frac{\left(x-2\right)\left(x+2\right)}{\left(x+3\right)\left(x-3\right)}\cdot\frac{3\left(x+3\right)}{x+2}=\frac{3\left(x-2\right)}{x-3}\)
\(\frac{x^3-8}{5x+20}\cdot\frac{x^2+4x}{x^2+2x+4}=\frac{\left(x-2\right)\left(x^2+2x+4\right)}{5\left(x+4\right)}\cdot\frac{x\left(x+4\right)}{x^2+2x+4}=\frac{x\left(x-2\right)}{5}\)
\(\frac{4x+12}{\left(x+4\right)^2}:\frac{3x+9}{x+4}=\frac{4\left(x+3\right)}{\left(x+4\right)^2}\cdot\frac{x+4}{3\left(x+3\right)}=\frac{4}{3\left(x+4\right)}\)

Bài 1: Đặt \(f\left(x\right)=\left(x^2+x+1\right)^{10}+\left(x^2-x+1\right)^{10}-2\)
Giả sử \(f\left(x\right)\)chia hết cho x-1
\(\Rightarrow f\left(x\right)=\left(x-1\right)q\left(x\right)\)
\(\Rightarrow f\left(1\right)=\left(1-1\right)q\left(1\right)\)
\(=0\)
\(\Leftrightarrow\left(1^2+1+1\right)^{10}+\left(1^2-1+1\right)^{10}-2=0\)
Mà \(\left(1^2+1+1\right)^{10}+\left(1^2-1+1\right)^{10}-2=59048\)
\(\Rightarrow\)mâu thuẫn
\(\Rightarrow f\left(x\right)\)không chia hết cho x-1 ( trái với đề bài )
Bài 2:
x^4-x^3-3x^2+ax+b x^2-x-2 x^2-1 x^4-x^3-2x^2 - - -x^2+ax+b -x^2+x+2 - (a-1)x+b-2
Vì \(x^4-x^3-3x^2+ax+b\)chia cho \(x^2-x-2\)dư \(2x-3\)
\(\Rightarrow\left(a-1\right)x+b-2=2x-3\)
Đồng nhất hệ số 2 vế ta được:
\(\hept{\begin{cases}a-1=2\\b-2=-3\end{cases}\Leftrightarrow}\hept{\begin{cases}a=3\\b=-1\end{cases}}\)
Vậy ...
Bài 3:
Vì \(P\left(x\right)\)chia \(x+3\)dư 1
\(\Rightarrow P\left(x\right)=\left(x+3\right)q\left(x\right)+1\)
\(\Rightarrow q\left(-3\right)=\left(-3+3\right)q\left(-3\right)+1\)
\(=1\left(1\right)\)
Vì \(P\left(x\right)\)chia \(x-4\)dư 8
\(\Rightarrow P\left(x\right)=\left(x-4\right)q\left(x\right)+8\)
\(\Rightarrow P\left(4\right)=\left(4-4\right)q\left(4\right)+8\)
\(=8\left(2\right)\)
Vì \(P\left(x\right)\)chia cho \(\left(x+3\right)\left(x-4\right)\)được thương là 3x và còn dư
\(\Rightarrow P\left(x\right)=\left(x+3\right)\left(x-4\right)3x+ax+b\left(3\right)\)
Từ (1) , (2) và (3) \(\Rightarrow\hept{\begin{cases}-3a+b=1\\4a+b=8\end{cases}\Leftrightarrow\hept{\begin{cases}-12a+3b=4\\12a+3b=24\end{cases}\Leftrightarrow}\hept{\begin{cases}b=4\\a=1\end{cases}\left(4\right)}}\)
Thay (4) vào (3) ta được:
\(P\left(x\right)=\left(x+3\right)\left(x-4\right)3x+x+4\)
\(\Leftrightarrow P\left(x\right)=3x^3-3x^2-20x+4\)

=(x.x^3-x.x^2-x.x+3.x)/(x.x-2x+1)
=x(x^3-x^2+x+3)/x(x-2+1)
=2x/x-1
(chắc lm như vầy)


a) \(\left( {6{x^3} - 7{x^2} - x + 2} \right):\left( {2x + 1} \right)\)

b) $(x^4-x^3+x^2+3x):(x^2-2x+3)$

c) \(\left( {{x^2} + {y^2} + 6x + 9} \right):\left( {x + y + 3} \right)\)
\(=\left( {{x^2} + 6x + 9 - {y^2}} \right)\left( {x + y + 3} \right)\)
\(=\left[ {\left( {{x^2} + 2x.3 + {3^2}} \right) - {y^2}} \right]:\left( {x + y + 3} \right)\)
\(=\left[ {{{\left( {x + 3} \right)}^2} - {y^2}} \right]:\left( {x + y + 3} \right)\)
\(=\left( {x + 3 - y} \right)\left( {x + 3 + y} \right):\left( {x + y + 3} \right)\)
$= x + 3 - y$
$= x - y + 3$
(6x3 - 7x2 - x + 2) : (2x + 1)
= (6x3 + 3x2 - 10x2 - 5x + 4x + 2) : (2x + 1)
= [(6x3 + 3x2) - (10x2 + 5x) + (4x + 2)] : (2x + 1)
= [3x2(2x + 1) - 5x(2x + 1) + 2(2x + 1)] : (2x + 1)
= (3x2 - 5x + 2)(2x + 1) : (2x + 1)
= 3x2 - 5x + 2
(x4 - x3 + x2 + 3x) : (x2 - 2x + 3)
= (x4 + x3 - 2x3 - 2x2 + 3x2 + 3x) : (x2 - 2x + 3)
= [(x4 + x3) - (2x3 + 2x2) + (3x2 + 3x)] : (x2 - 2x + 3)
= [x3(x + 1) - 2x2(x + 1) + 3x(x + 1)] : (x2 - 2x + 3)
= (x3 - 2x2 + 3x)(x + 1) : (x2 - 2x + 3)
= x(x2 - 2x + 3)(x + 1): (x2 - 2x + 3)
= x(x + 1)
= x2 + x
(x2 - y2 + 6x + 9) : (x + y + 3)
= [(x2 + 6x + 9) - y2] : (x + y + 3)
= [(x + 3)2 - y2] : (x + y + 3)
= (x + 3 + y)(x + 3 - y) : (x + y + 3)
= (x + y + 3)(x - y + 3) : (x + y + 3)
= x - y + 3
CHÚC BN HOK TỐT ![]()
![]()
![]()