Không dùng bảng lượng giác và máy tính bỏ túi, hãy so sánh: tg...

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

Pham Trong Bach

9 tháng 3 2017

Không dùng bảng lượng giác và máy tính bỏ túi, hãy so sánh: tg 32 ° và cos 58 °

#Toán lớp 9

Cao Minh Tâm

9 tháng 3 2017

Đúng(0)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

Sách Giáo Khoa

27 tháng 4 2017

Không dùng bảng lượng giác và máy tính bỏ túi, hãy so sánh :

a) \(tg28^0\) và \(\sin28^0\)

b) \(cotg42^0\) và \(\cos42^0\)

c) \(cotg73^0\) và \(\sin17^0\)

d) \(tg32^0\) và \(\cos58^0\)

#Toán lớp 9

Ứ Cờ Ức Đờ Ức Đưc Sắc Đức

18 tháng 10 2017

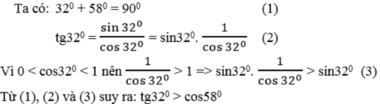
a) tg28∘=sin28∘cos28∘=sin28∘.1cos28∘tg28∘=sin⁡28∘cos⁡28∘=sin⁡28∘.1cos⁡28∘ (1)

Vì 0 < cos28° < 1 nên 1cos28∘>1⇒sin28∘.1cos28∘>sin28∘1cos⁡28∘>1⇒sin⁡28∘.1cos⁡28∘>sin⁡28∘ (2)

Từ (1) và (2) suy ra: tg28° > sin28°

b) Ta có: cotg42∘=cos42∘sin42∘=cos42∘.1sin42∘cot⁡g42∘=cos⁡42∘sin⁡42∘=cos42∘.1sin⁡42∘ (1)

Vì 0 < sin42° < 1 nên 1sin42∘>1⇒cos42∘.1sin42∘>cos42∘1sin⁡42∘>1⇒cos⁡42∘.1sin⁡42∘>cos⁡42∘ (2)

Từ (1) và (2) suy ra: cotg42° > cos42°

c) Ta có: 17° +73° =90° (1)

cotg73∘=cos73∘sin73∘=cos73∘.1sin73∘cot⁡g73∘=cos⁡73∘sin⁡73∘=cos⁡73∘.1sin⁡73∘ (2)

Vì 0 <sin73° <1 nên 1sin73∘>1⇒cos73∘.1sin73∘>cos73∘1sin⁡73∘>1⇒cos73∘.1sin⁡73∘>cos73∘ (3)

Từ (1), (2) và (3) suy ra: cotg73° > sin17°

d) Ta có: 32° +58° = 90° (1)

tg32∘=sin32∘cos32∘=sin32∘.1cos32∘tg32∘=sin⁡32∘cos⁡32∘=sin⁡32∘.1cos⁡32∘ (2)

Vì 0 < cos32° < 1 nên 1cos32∘>1⇒sin32∘.1cos32∘>sin32∘1cos32∘>1⇒sin⁡32∘.1cos32∘>sin⁡32∘ (3)

Từ (1), (2) và (3) suy ra: tg32° > cos58°

Đúng(0)

Sách Giáo Khoa

27 tháng 4 2017

Không dùng bảng lượng giác và máy tính bỏ túi, hãy so sánh :

a) \(tg50^028'\) và \(tg63^0\)

b) \(cotg14^0\) và \(cotg35^012'\)

c) \(tg27^0\) và \(cotg27^0\)

d) \(tg65^0\) và \(cotg65^0\)

#Toán lớp 9

Nguyễn Lê Phước Thịnh

16 tháng 5 2022

a: \(\tan50^028'< \tan63^0\)

b: \(\cot14^0>\cot35^012'\)

c: \(\tan27^0=\cot63^0< \cot27^0\)

d: \(\tan65^0=\cot25^0>\cot65^0\)

Đúng(0)

Sách Giáo Khoa

27 tháng 4 2017

Không dùng bảng lượng giác và máy tính bỏ túi, hãy so sánh :

a) \(\sin25^0\) và \(\sin70^0\)

b) \(\cos40^0\) và \(\cos75^0\)

c) \(\sin38^0\) và \(\cos27^0\)

d) \(\sin50^0\) và \(\cos50^0\)

#Toán lớp 9

Nguyễn Lê Phước Thịnh

16 tháng 5 2022

a: \(\sin25^0< \sin70^0\)

b: \(\cos40^0>\cos75^0\)

c: \(\sin38^0=\cos52^0< \cos27^0\)

d: \(\sin50^0=\cos40^0>\cos50^0\)

Đúng(0)

Sách Giáo Khoa

24 tháng 4 2017

Dùng bảng lượng giác hoặc máy tính bỏ túi để tìm góc nhọn x (làm tròn kết quả đến độ), biết rằng :

a) \(\sin x=0,3495\)

b) \(\cos x=0,5427\)

c) \(tg=1,5142\)

d) \(cotgx=3,163\)

#Toán lớp 9

Nhật Linh

24 tháng 4 2017

ĐS: a) x≈20∘x≈20∘;

b) x≈57∘x≈57∘;

c) x≈57∘x≈57∘;

d) x≈18∘x≈18∘.

Đúng(0)

Nguyễn Đinh Huyền Mai

24 tháng 4 2017

a) x≈20∘x≈20∘;

b) x≈57∘x≈57∘;

c) x≈57∘x≈57∘;

d) x≈18∘x≈18∘.

Đúng(0)

Sách Giáo Khoa

23 tháng 4 2017

So sánh (không dùng bảng số hay máy tính bỏ túi)

\(\sqrt{2003}+\sqrt{2005}\) và \(2\sqrt{2004}\)

#Toán lớp 9

Lưu Hạ Vy

23 tháng 4 2017

Đặt A = \(\sqrt{ }\)2003 + \(\sqrt{ }\)2005 ; B = 2\(\sqrt{ }\)2004
A² = 2003 + 2005 + 2\(\sqrt{ }\)(2003.2005)
= 4008 + 2\(\sqrt{ }\)[(2004-1)(2004+1)]
= 4008 + 2\(\sqrt{ }\)(2004² - 1) < 2.2004 + 2\(\sqrt{ }\)(2004²) = 4.2004 = B²
\(\Rightarrow\) A < B