Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
Đặt m là khối lượng tấm ván, ∆m là khối lượng hòn đá. Do cả hai trường hợp đều trượt đều (a = 0) nên ta có:

Có thể giải thích cho mik tại sao lại ra 0,2 được không. Sao mik thay số vào ko đc

\(\overrightarrow{F}+\overrightarrow{F}_{ms}=\overrightarrow{N}+\overrightarrow{P}=m\overrightarrow{a}\)
Phương vuông góc mp nghiêng:
\(N=Pcos45\)
Phương mp nghiêng
\(F-F_{ms}=Psin45=ma\)
\(F=ma-F_{ms}+Psin45=14+0,2.10.1cos45+10.1sin45\)
\(=12,485N\)

theo định luật II niu tơn
\(\overrightarrow{F}+\overrightarrow{F_{ms}}+\overrightarrow{N}+\overrightarrow{P}=m.\overrightarrow{a}\)
chiếu lên trục Ox phương nằm ngang chiều dương cùng chiều chuyển động
F-\(\mu.m.g=m.a\) (theo phương Oy thì N=P=m.g)
\(\Rightarrow a=\)1m/s2
A.

a) theo định luật II niu tơn
\(\overrightarrow{F}+\overrightarrow{F_{ms}}+\overrightarrow{N}+\overrightarrow{P}=m.\overrightarrow{a}\)
chiếu lên trục Ox phương nằm ngang chiều dương cùng chiều chuyển động
F.cos\(\alpha\)-\(\mu.N=0\) (1) (a=0, vật chuyển động đều)
chiếu lên trục Oy phương thẳng đứng chiều dương hướng lên trên
N=P-\(sin\alpha.F\) (2)
từ (1),(2)\(\Rightarrow F\approx103,5N\)
b) từ câu a ta có
\(F.cos\alpha-\mu.\left(P-sin\alpha.F\right)=0\)
\(\Leftrightarrow F=\dfrac{\mu.P}{cos\alpha+\mu.sin\alpha}\)
đặt \(\mu\)=\(tan\beta=\dfrac{sin\beta}{cos\beta}\) (\(0^0< \beta< 90^0\)
để F min thì MS= \(cos\alpha+\mu.sin\alpha\) max (MS: mẫu số)
\(\Leftrightarrow\)MS=\(\dfrac{cos\alpha.cos\beta+sin\beta.sin\alpha}{cos\beta}\)=\(\dfrac{cos\left(\alpha-\beta\right)}{cos\beta}\)
MS max khi \(cos\left(\alpha-\beta\right)\)=1 (vì \(cos\beta\) ở dưới mẫu min thì MS max nhưng cos\(\beta\) min ko xác định được )
\(cos\left(\alpha-\beta\right)=1\Leftrightarrow\alpha-\beta=0\)
\(\Leftrightarrow\alpha=\beta\)
\(\Rightarrow tan\alpha=tan\beta=\mu=0,2\)
\(\Rightarrow\alpha\approx11,3^0\)

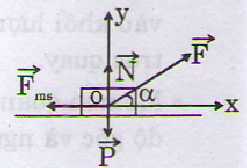
Lực tác dụng lên vật m được biểu diễn trên hình vẽ.
Định luật II Niu-tơn cho:
Chọn hệ trục Oxy với chiều dương là chiều chuyển động theo phương Ox, chiếu phương trình (1) lên:
(Ox): Fcosα- fms= ma (2)
(Oy): N + Fsinα – P = 0 (3)
mà fms= μN (4)
(2), (3) và (4) => F cosα – μ(P- Fsinα ) = ma
=> Fcosα – μP + μFsinα = ma
F(cosα +μsinα) = ma +μmg
=> F =
a) khi a = 1,25 m/s2


theo định luật II niu tơn
\(\overrightarrow{F}+\overrightarrow{F_{ms}}+\overrightarrow{N}+\overrightarrow{P}=m.\overrightarrow{a}\) (1)
chiếu (1) lên trục Ox phương nằm ngang chiều dương cùng chiều chuyển động
F-Fms=0 (a=0, vật trượt đều) (2)
chiếu (1) lên trục Oy phương nằm ngang chiều dương hương lên trên
N=P=m.g (3)
từ (2),(3)
\(\Rightarrow\mu=\)0,2

a) Vật chuyển động nhanh dần đều \(\Rightarrow\) áp dụng định luật II Newton:
Gia tốc của thùng:
(3): \(S=V_0.t+\dfrac{1}{2}at^2\) \(\Rightarrow\) \(a=2\) m/\(s^2\)
Cho \(g=10\) m/\(s^2\)
Chiếu hình vẽ lên trục Ox (tự vẽ):
Theo Ox: \(a=\dfrac{F-F_{mst}}{m}=\dfrac{225-F_{mst}}{50}\)
\(\Rightarrow\) \(F_{mst}=125N\)
mà: \(F_{mst}=\mu.N=\mu.m.g\) \(\Rightarrow\) \(\mu=\dfrac{125}{10.50}=0,25\)
b) Vật chuyển động thẳng đều \(\Rightarrow\) Áp dụng đinh luật I Newton:
\(F=F_{mst}=125N\)


Chọn B.
Đặt m là khối lượng tấm ván, ∆m là khối lượng hòn đá. Do cả hai trường hợp đều trượt đều (a = 0) nên ta có: