Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Do đó, \(SD=\dfrac{a^2}{2}:a\sqrt{2}=\dfrac{a\sqrt{2}}{4}\)
và \(AD=SA-SD=\dfrac{3a\sqrt{2}}{4}\)

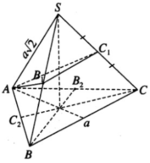
Giả sử mặt cầu đi qua đỉnh A của hình chóp và tiếp xúc với cạnh SB tại B1, tiếp xúc với cạnh SC tại C 1 . Khi đó mặt cầu cắt cạnh AB, AC lần lượt tại các điểm C 2 , B 2 . Mặt phẳng (SAB) cắt mặt cầu đó theo giao tuyến là một đường tròn. Đường tròn này tiếp xúc với SB tại B1 và đi qua A và C 2
Do đó, ta có: BB 1 2 = BA . BC 2
trong đó 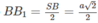
Do đó 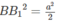
Vậy
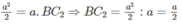
Điều đó chứng tỏ mặt cầu nói trên đi qua trung điểm C 2 của đoạn AB. Lí luận tương tự ta chứng minh được mặt cầu đó đi qua trung điểm B 2 của AC.

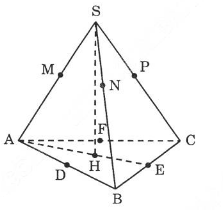
Gọi M, N, P theo thứ tự là các tiếp điểm của mặt cầu với các cạnh SA, SB, SC; D, E, F theo thứ tự là trung điểm của các cạnh AB, BC, CA, các điểm D, E, F đồng thời cũng là tiếp điểm của mặt cầu với các cạnh AB, BC, CA.
Ta có: AD = AF => AB = AC⇒=> AB = AC
BD = BE=>⇒ BC = AB
=>⇒ AB = BC = CA
=>⇒ \(\Delta ABC\) là tam giác đều (1)
Ta lại có AM = AD; BN = BD = AD
và SM = SN = SP
=>⇒ SM + AM = SN + NB
=>⇒ SA = SB
Chứng minh tương tự ta có: SA = SB = SC.
Gọi H là chân đường cao của hình chóp kẻ từ đỉnh S, ta có:
\(\Delta SHA=\Delta SHB=\Delta SHC\) =>⇒ HA = HB = HC
=>⇒ H là tâm của tam giác đều ABC (2)
Từ (1) và (2) suy ra hình chóp S.ABC là hình chóp tam giác đều.

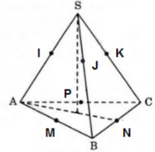
Gọi mặt cầu đã cho có tâm O và bán kính R.
Gọi M, N, P lần lượt là trung điểm của AB, BC và CA.
Gọi I,J và K lần lượt là tiếp điểm của các cạnh bên SA, SB, SC với mặt cầu:
+ Từ giả thiết ta suy ra: OI ⊥ SA; OM ⊥ AB
Xét tam giác OIA và tam giác OMA có:
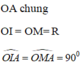
⇒ ∆ OIA = ∆OMA ( ch- cgv)
⇒ AM = AI.
Chứng minh tương tự có: BM= BJ và SI = SJ (1)
Mà AM = BM nên AI= BJ ; (2)
Từ (1) và (2) suy ra: SI+IA = SJ + BJ hay SA = SB (3)
* Chứng minh tương tự, ta có SB= SC (4).
Từ (3) và (4) suy ra: SA = SB = SC (*)
Mặt khác ; BM = BN (= BJ) và CN = CP (= CK)
Suy ra; AB = 2BM = BC = 2 CN = 2CP = CA
Do đó, tam giác ABC là tam giác đều (**)
Từ (*) và (**) suy ra, S. ABC là hình chóp tam giác đều.

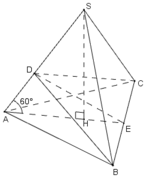
a)
+ Gọi H là hình chiếu của S trên (ABC)
⇒ AH là hình chiếu của SA trên (ABC)
Gọi E là trung điểm BC
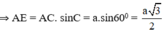
H là tâm của Δ đều ABC.


+)Gọi H là chân đường cao hạ từ A - -> BC
Tam giác AHC vuông tại H nên
AH = √(a² -a²/4) = a√3/2
Diện tích tam giác ABC là S(ABC) = 1/2.AH.BC= 1/2.a²√3/2
(dvdt)
+)Từ S hạ SK ┴ AH , Kết hợp AH ┴ BC ta có SK ┴ (ABC)
Hay SK là đường cao của hình chóp đều SABC
+) Bài cho góc giữa các mặt bên với đáy là 60 độ nên
góc giữa (SH,HK) = 60 độ
Tam giác vuông SKH có SK = HK.tan(60)
Tam giác vuông BKH có HK = a/2.tan(30) = a√3/6
- - > SK = a√3/6.tan(60) = a/2
Vậy V(SABC) =1/3.SK.S(ABC) = 1/3.a/2.1/2.a²√3/2
= a³√3/24 (dvtt)

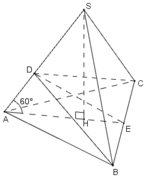
S H = S A 2 - A H 2 = a
Thể tích khối chóp S.ABC là:
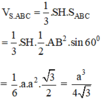
⇒ Thể tích khối chóp S.DBC là:
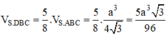

ình chóp S.ABCD là hình chóp đều nên chân H của đường cao SH chính là tâm của đáy. Mặt phẳng đi qua AM và song song với BD cắt mặt phẳng (SDB) theo một giao song song với BD, hay EF // BD.
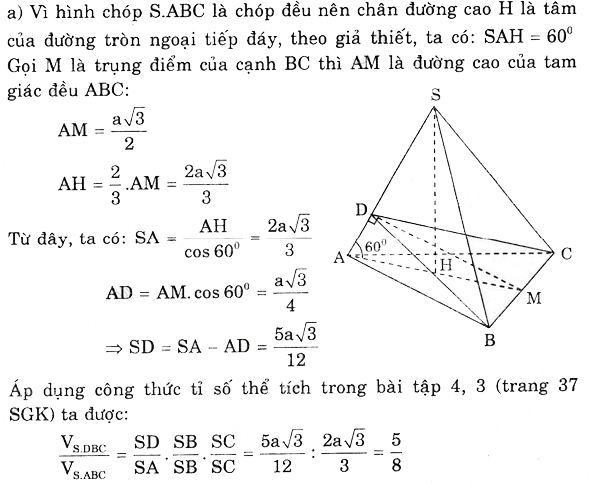
Ta dựng giao tuyến EF như sau : Gọi I là giao điểm của AM và SH Qua I ta dựng một đường thẳng song song với BD, đường này cắt SB ở E và cắt SD ở F. Ta có góc SAH= 60°. Tam giác cân SAC có SA = SC và SAC = 60° nên nó là tam giác đều: I là giao điểm của các trung tuyến AM và SH nên:

Gọi giao điểm thứ hai của mặt cầu với đường thẳng SA là D, ta có:
Do đó