Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số hình lập phương ở hình 1: 1.3+1.1.2=5 (khối)
Số hình lập phương ở hình 2:22.3+22.2.2=28 (khối)
Số hình lập phương ở hình 3:32.3+32.3.2=81 (khối)
\(\Rightarrow\)Công tức tính:
Số hình lập phương ở hình x: x2.3+x2.x.2 (khối)
Số hình lập phương ở hình 10 là:102.3+102.10.2=2300 (khối)
Cách 1 : Khi ta vẽ hình thứ tư thì :
Số hình lập phương đơn vị ở phía trái là 4.5.4=80


a)Ta có E là trung điểm của CM (gt)
F là trung điểm của CB (gt)
\(\Rightarrow\) EF là đường trung bình của (định nghĩa đường trung bình của tam giác)
\(\Rightarrow\) EF//MB (tính chất đường trung bình của tam giác)
hay EF//AB
lại có K là trung điểm của AD (gt)
F là trung điểm của CB (gt)
\(\Rightarrow\) KF là đường trung bình của (...)
\(\Rightarrow\) KF//AM (t/c ...)
hay KF//AB
nên EF//KF (vì cùng // với AB)
\(\Rightarrow\) tứ giác EFFIK là hình thang (Định nghĩa hình thang)
Gọi N là trung điểm của AM, nối KM
Ta có N là trung điểm của AM (cách dựng)
K là trung điểm của AD (gt)
\(\Rightarrow\) NK là đường trung bình của
nên NK//DM (t/c....)
mà EN là đường trung bình của (E,I là trung điểm của MC,AM)
\(\Rightarrow\) EI//AC (t/c...)
lại có và
là những tam giác đều (gt)
\(\Rightarrow\)
\(\Rightarrow\) AC//DM
tức là NK//EN (cùng //AC//DM)
do đó 3 điểm E,K,N thẳng hàng (theo tiên đề Ơ-clit)
(2góc đồng vị của AC//EN)
(2 góc đồng vị của KF//AM)
nên
C/m tương tự, lấy P là trung điểm của BM ta cũng được
Hình thang EFIK có
Vậy EFIK là hình thang cân (dấu hiệu nhận biết)
b) Ta có EFIK là hình thang cân (kq câu a)
\Rightarrow EI=KF (tính chất 2 đường chéo trong hình thang cân)
E là trung điểm của CM, I là trung điểm của DM (gt)
\(\Rightarrow\) EI là đường trung bình của tam giác CMD
\(\Rightarrow\) EI=
Vậy KF=

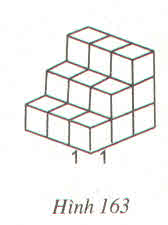
Lớp dưới cùng gồm: 3.3 (hình lập phương đơn vị)
Lớp ở giữa gồm: 3.2 (hình lập phương đơn vị)
Lớp trên cùng: 3 (hình lập phương đơn vị)
Tổng cộng có 9+6+3=18 (hình lập phương đơn vị)

gọi cạnh hình vuông thứ nhất là x (cm)
"""vì chu vi hình vuông thứ nhất kém chu vi hình vuông thứ hai là 16cm nên ta có:
4x=(chu vi hình vuông thứ 2)-16
=> x= (cạnh hình vuông thứ hai) - 4 (vì chu vi = 4 . cạnh)""""
=> cạnh hình vuông thứ hai thứ x+4
vì hiệu diện tích hai hình vuông này là 64cm vuông nên ta có phương trình:
(x+4)^2 - x^2= 64
=> x^2+8x+16 -x^2=64
=> 8x+16=64
=> 8x=48
=> x=6
vậy diện tích hình vuông thứ nhất là : 6^2=36cm vuông
diện tích hình vuông thứ hai là: (6+4)^2=100cm vuông
nếu bạn hiểu rùi thì không cần ghi phần bạn đã"""......."""" nhé
chúc bạn học tốt

17. Nửa chu vi miếng đất là: \(48:2=24\left(m\right)\)
Gọi chiều rộng, chiều dài miếng đất ban đầu lần lượt là a (m) và b (m) \(\left(0< a;b< 24\right)\)
Theo bài ra, ta có:
\(\hept{\begin{cases}a+b=24\\\left(a-2\right)\left(b+6\right)-ab=12\end{cases}}\Leftrightarrow\hept{\begin{cases}a+b=24\\6a-2b=24\end{cases}}\Leftrightarrow\hept{\begin{cases}a=9\\b=15\end{cases}}\)(thỏa mãn)
Diện tích miếng đất ban đầu là: \(a.b=9.15=135\left(m^2\right)\)

Bài 64 (trang 100 SGK Toán 8 Tập 1): Cho hình bình hành ABCD. Các tia phân giác của các góc A, B, C, D cắt nhau như trên hình 91. Chứng minh rằng EFGH là hình chữ nhật.
Theo giả thiết ABCD là hình bình hành nên ta có:
ˆDAB=ˆDCB,ˆADC=ˆABC (1)
Theo định lí tổng các góc của một tứ giác ta có:
ˆDAB+ˆDCB+ˆADC+ˆABC=360o (2)
Từ (1) và (2) ⇒ˆDAB+ˆABC=360o/2=180o
Vì AG là tia phân giác ˆDAB (giả thiết)
⇒⇒ ˆBAG=1/2ˆDAB (tính chất tia phân giác)
Vì BG là tia phân giác ˆABC (giả thiết)
⇒⇒ ˆABG=1/2ˆABC
Do đó: ˆBAG+ˆABG=1/2(ˆDAB+ˆABC)=1/2.1800=90o
Xét ΔAGB= có:
ˆBAG+ˆABG=90o (3)
Áp dụng định lí tổng ba góc trong một tam giác vào tam giác AGBAGB ta có:
ˆBAG+ˆABG+ˆAGB=180o (4)
Từ (3) và (4) ⇒ˆAGB=90o
Chứng minh tương tự ta được: ˆDEC=ˆEHG=90o
Tứ giác EFGH có ba góc vuông nên là hình chữ nhật (dấu hiệu nhận biết hình chữ nhật)
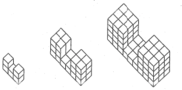
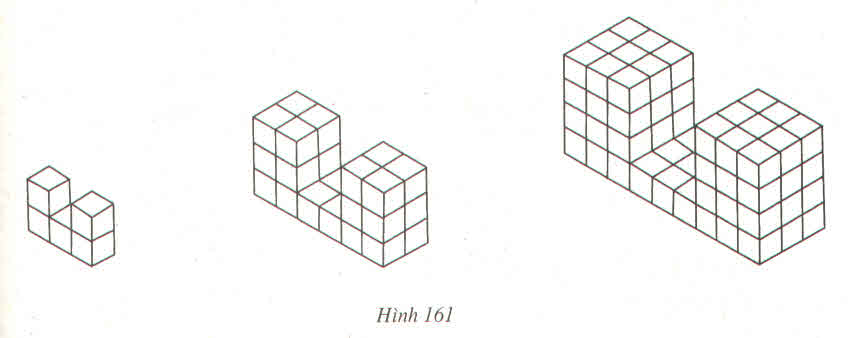




Khi vẽ hình thứ 3,ta có:
Số hình lập phương đơn vị bên trái là 3.4.3=36
Số hình lập phương đơn vị bên trái là 3.4.3 =36
Số hình lập phương đơn vị ở giữa là 3.3=9
Vậy có tổng số :36+36+9=81 hình lập phương đơn vị
Với quy luật đó thì hình thứ 10:
Số hình lập phương đơn vị bên trái là 10.11.10=1100
Số hình lập phương đơn vị bên trái là 10.11.10=1100
Số hình lập phương đơn vị ở giữa là 10.10 =100
Vậy tổng số hình lập phương đơn vị của hình thứ 10 là:
1100 + 1100 +100=2300 (hình)