Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(_1^1p + _4^9Be \rightarrow _2^4He + _3^6X\)
Áp dụng định luật bảo toàn động lượng \(\overrightarrow P_p=\overrightarrow P_{He}+ \overrightarrow P_{X} \) (do hạt Be đứng yên)
PPPHeXp
Dựa vào hình vẽ ta có \(P_{p}^2+ P_{He}^2 = P_X^2\)
=> \(2m_{p}K_{p}+2m_{He} K_{He} = 2m_{X}K_{X}. \)
=> \(K_{p}+4K_{He} = 6K_{X} => K_X = 6MeV.\)

\(\alpha + _7^{14}N \rightarrow _1^1p + _8^{17}O\)
\(m_t-m_s = m_{\alpha}+m_N - (m_{O}+m_p) =- 1,3.10^{-3}u < 0\), phản ứng thu năng lượng.
\(W_{thu} = (m_s-m_t)c^2 = K_t-K_s\)
=> \(1,3.10^{-3}.931,5 = K_{He}+K_N- (K_p+K_O)\)(do Nito đứng yên nên KN = 0)
=> \(K_p +K_O = 6,48905MeV. (1)\)
Áp dụng định luật bảo toàn động lượng
P P α P p O
\(\overrightarrow P_{\alpha} =\overrightarrow P_{p} + \overrightarrow P_{O} \)
Dựa vào hình vẽ ta có (định lí Pi-ta-go)
\(P_{O}^2 = P_{\alpha}^2+P_p^2\)
=> \(2m_{O}K_{O} = 2m_{He}K_{He}+ 2m_pK_p.(2)\)
Từ (1) và (2) giải hệ phương trình ta được
\(K_p = 4,414MeV; K_O = 2,075 MeV.\)

\(_1^1p + _4^9Be \rightarrow _2^4He+ _3^6 Li\)
Áp dụng định luật bảo toàn động lượng
PPαPLip
\(\overrightarrow P_{p} =\overrightarrow P_{He} + \overrightarrow P_{Li} \)
Dựa vào hình vẽ ta có (định lí Pi-ta-go)
\(P_{Li}^2 = P_{\alpha}^2+P_p^2\)
=> \(2m_{Li}K_{Li} = 2m_{He}K_{He}+ 2m_pK_p\)
=> \(K_{Li} = \frac{4K_{He}+K_p}{6}=3,58MeV\)
=> \(v = \sqrt{\frac{2.K_{Li}}{m_{Li}}} = \sqrt{\frac{2.3,58.10^6.1,6.10^{-19}}{6.1,66055.10^{-27}}} = 10,7.10^6 m/s.\)

\(_1^1p + _4^9Be \rightarrow \alpha + _3^6Li\)
Phản ứng này thu năng lượng => \(W_{thu} =(m_s-m_t)c^2 = K_t-K_s\)
=> \( K_p+ K_{Be}-K_{He}- K_{Li} = W_{thu} \) (do Be đứng yên nên KBe = 0)
=> \(K_p = W_{thu}+K_{Li}+K_{He} = 2,125+4+3,575 = 9,7MeV.\)
Áp dụng định luật bảo toàn động lượng
P P P α α p Li
\(\overrightarrow P_{p} =\overrightarrow P_{He} + \overrightarrow P_{Li} \)
Dựa vào hình vẽ ta có
Áp dụng định lí hàm cos trong tam giác
=> \(\cos {\alpha} = \frac{P_p^2+P_{He}^2-P_{Li}^2}{2P_pP_{He}} = \frac{2.1.K_p+ 2.4.K_{He}-2.6.K_{Li}}{2.2.2m_pm_{He}K_pK_{He}} = 0.\)
Với \(P^2 = 2mK, m=A.\).
=> \(\alpha = 90^0.\)

\(_2^4 He + _{13}^{27}Al \rightarrow _{15}^{30}P + _0^1n\)
Phản ứng thu năng lượng
\( K_{He} - (K_{P}+K_{n} )= 2,7MeV.(*)\)
Lại có \(\overrightarrow v_P = \overrightarrow v_n .(1)\)
=> \(v_P = v_n\)
=> \(\frac{K_P}{K_n} = 30 .(2)\)
Áp dụng định luật bảo toàn động lượng trước và sau phản ứng
\(\overrightarrow P_{He} = \overrightarrow P_{P} + \overrightarrow P_{n} \)
Do \(\overrightarrow P_{P} \uparrow \uparrow \overrightarrow P_{n}\)
=> \(P_{He} = P_{P} + P_{n} \)
=> \(m_{He}.v_{He} = (m_{P}+ m_n)v_P=31m_nv\) (do \(v_P = v_n = v\))
=> \(K_{He} = \frac{31^2}{4}K_n.(3)\)
Thay (2) và (3) vào (*) ta có
\(K_{He}-31K_n= 2,7.\)
=> \(K_{He} = \frac{2,7}{1-4/31} = 3,1MeV.\)

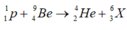
Vì hạt Be đứng yên nên theo định luật bảo toàn động lượng
Đáp án A

Đáp án C
Phương pháp:
Sử dụng định luật bảo toàn số khối và bảo toàn điện tích để viết phương trình phản ứng.
Sử dụng định luật bảo toàn động lượng trong phản ứng hạt nhân.
Công thức liên hê ̣giữa động lượng và động năng: p 2 = 2mK
Công thức tính năng lượng toả ra của phản ứng: ∆E = (mt – ms)c2 = Ks - Kt
(Kt, Ks lần lượt là tổng động năng của các hạt trước vàsau phản ứng)
Cáchgiải
+ PT phản ứng:
![]()
+ Theo định luật bảo toàn động lượng ta có:
![]()
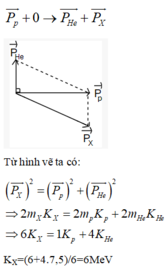
ta biểu diễn bằng hình vẽ sau
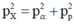
Từ hình vẽ ta có:
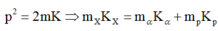
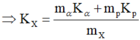
Năng lượng tỏa ra của phản ứng :
![]()
![]()

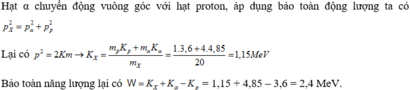
Chọn A