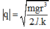Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
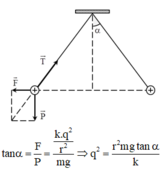
Ở vị trí cân bằng mỗi quả cầu sẽ chịu tác dụng của 3 lực: trọng lực P → , lực tĩnh điện F → và sức căng sợi dây T → .
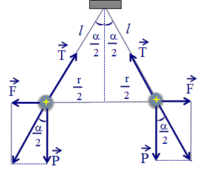
Khi đó: tan α = F P = k q 2 r 2 m g = k q 2 m g r 2 (1).
Mặt khác, vì r << l nên a là rất nhỏ, do đó:
tan α ≈ sin α = r 2 l ( 2 ) . T ừ ( 1 ) v à ( 2 ) s u y r a q = m g r 3 2 l k
a) Chiều lên phương của sợi dây:
\(T\cos a=P=mg\)
\(T\sin a=F\left(F=kq_1.\frac{q_2}{r^2}\right)\)
Mà hai quả nhiểm điên như nhau.
\(\Rightarrow q_1=q_2=q\Rightarrow F=mg.\tan a\)
a là góc lệch sợi dây phương ngang.
Có: \(\sin a=\frac{r}{\left(2l\right)}\)
Vì a rất nhỏ \(\Rightarrow\sin a=\tan a=\frac{3}{50}\)
Thay vào ra \(F=3,6.10^{-4}\Rightarrow q=1,2.10^{-8}C\)
b) Lúc này: \(F=\frac{k.q^2}{e.r^2}\)
Với e là hằng số điện mới.
\(\Rightarrow F=\frac{mg.q^2}{er^2}=mg.\tan a=mg.\sin a=\frac{mg.r'}{2l'}\)
Thay vào tính được r' = 20 cm
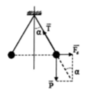
Góc lệch \(\alpha\) của dây treo được xác định bằng hệ thức (suy từ điều kiện cân bằng của hai quả cầu :)
\(\tan\alpha=\frac{F_đ}{P}\)
Với \(F_đ=k\frac{q^2}{a^2}\) Như vậy \(\tan\alpha=\frac{kq^2}{mga^2}\)
Thay số ta được : \(\tan\alpha=1\) suy ra \(\alpha=45^o\)
mình chưa hiểu đoạn tan a = F/P lắm bạn giải thích lại hộ mình đc ko
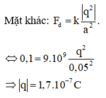
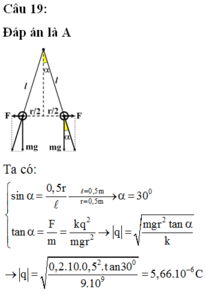
Đáp án: A
Ở vị trí cân bằng mỗi quả cầu sẽ chịu tác dụng của ba lực: trọng lực P → , lực tĩnh điện F → và lực căng dây T → . Khi đó:
Vì r rất nhỏ so với ℓ nên α nhỏ
Ta có
do vậy độ lớn của điện tích đã truyền cho quả cầu là: 