
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

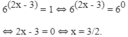

a) Chia 2 vế của phương trình cho \(5^x>0\), ta có :
\(\left(\frac{3}{5}\right)^x+\left(\frac{4}{5}\right)^x=1\)
Xét \(f\left(x\right)=\left(\frac{3}{5}\right)^x+\left(\frac{4}{5}\right)^x\)
Ta có :
\(f'\left(x\right)=\left(\frac{3}{5}\right)^x\ln\frac{3}{5}+\left(\frac{4}{5}\right)^x\ln\frac{4}{5}<0\) với mọi x
Do đó \(f\left(x\right)\) đồng biến trên R
Mặt khác
f(2) =1. Do đó x=2 là nghiệm duy nhất của phương trình
b) Phương trình tương đương với
\(2^x\left(2-2^x\right)=x-1\)
Với x=1 thì phương trình trên đúng, do đó x=1 là nghiệm của phương trình
- Nếu x>1 thì \(2<2^x\) và \(x-1>0\) do đó \(2^x\left(2-2^x\right)<0\)< \(x-1\)
phương trình vô nghiệm
- Nếu x<1 thì \(2>2^x\) và \(x-1<0\) do đó \(2^x\left(2-2^x\right)>0\)> \(x-1\)
phương trình đã cho có 1 nghiệm duy nhất là x=1

a) Tập xác định : D = R
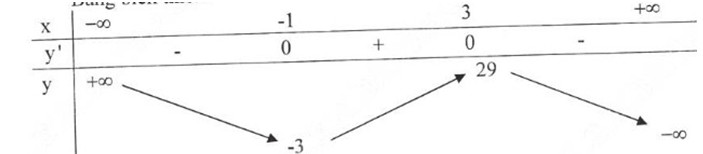
limx→−∞f(x)=+∞limx→+∞f(x)=−∞y′=−3x2+6x+9=0⇔x=−1,x=3limx→−∞f(x)=+∞limx→+∞f(x)=−∞y′=−3x2+6x+9=0⇔x=−1,x=3
Bảng biến thiên:
Đồ thị hàm số:
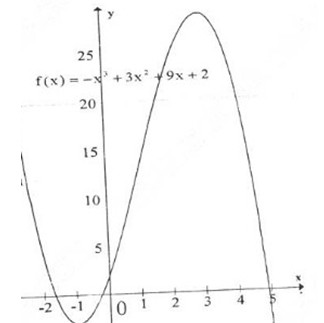
b) y=f(x) = f(x) = -x3+3x2+9x+2.
f’(x) = -3x2+6x+9. Do đó:
f’(x-1)=-3(x-1)2+6(x-1)+9
= -3x2 + 12x = -3x(x-4) > 0 ⇔ 0 < x < 4
c) f’’(x) = -6x+6
f’’(x0) = -6 ⇔ -6x0 + 6 = -6 ⇔ x0 = 2
Do đó: f’(2) = 9, f(2) = 24. Phương trình tiếp tuyến của (C) tại x0 = 2 là:
y=f’(2)(x-2) + f(2) hay y = 9x+6

a) Điều kiện \(x-4>0\Leftrightarrow x>4\)
Đặt \(f\left(x\right)=lg\left(x-4\right),g\left(x\right)=5-x\)
Phương trình đã cho trở thành
\(f\left(x\right)=g\left(x\right)\)
Ta có \(f\left(x\right)\) đồng biến trên \(\left(4;+\infty\right)\) và \(g\left(x\right)\) nghịch biến trên R
Hơn nữa \(f\left(5\right)=g\left(5\right)\) do đó \(x=5\) là nghiệm duy nhất của phương trình
b) Dễ thấy \(x=\sqrt{2}\) là nghiệm của phương trình.
Nếu \(x>\sqrt{2}\) thì \(x^x>\left(\sqrt{2}\right)^x>\left(\sqrt{2}\right)^{\sqrt{2}}\)
Tương tự \(x<\sqrt{2}\) . Vậy \(x=\sqrt{2}\) là nghiệm duy nhất